Find maximum points which can be obtained by deleting elements from array
Last Updated :
15 Jan, 2023
Given an array A having N elements and two integers L and R where, 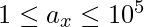 and
and 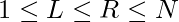 . You can choose any element of the array (let’s say ax) and delete it, and also delete all elements equal to ax+1, ax+2 … ax+R and ax-1, ax-2 … ax-L from the array. This step will cost ax points. The task is to maximize the total cost after deleting all the elements from the array.
. You can choose any element of the array (let’s say ax) and delete it, and also delete all elements equal to ax+1, ax+2 … ax+R and ax-1, ax-2 … ax-L from the array. This step will cost ax points. The task is to maximize the total cost after deleting all the elements from the array.
Examples:
Input : 2 1 2 3 2 2 1
L = 1, R = 1
Output : 8
We select 2 to delete, then (2-1)=1 and (2+1)=3 will need to be deleted,
for given L and R range respectively.
Repeat this until 2 is completely removed. So, total cost = 2*4 = 8.
Input : 2 4 2 9 5
L = 1, R = 2
Output : 18
We select 2 to delete, then 5 and then 9.
So total cost = 2*2 + 5 + 9 = 18.
Approach: We will find the count of all the elements. Now let’s say an element X is selected then, all elements in the range [X-L, X+R] will be deleted. Now we select the minimum range from L and R and finds up to which elements are to be deleted when element X is selected. Our results will be the maximum of previously deleted elements and when element X is deleted. We will use dynamic programming to store the result of previously deleted elements and use it further.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int maxCost(int a[], int n, int l, int r)
{
int mx = 0, k;
for (int i = 0; i < n; ++i)
mx = max(mx, a[i]);
int count[mx + 1];
memset(count, 0, sizeof(count));
for (int i = 0; i < n; i++)
count[a[i]]++;
int res[mx + 1];
res[0] = 0;
l = min(l, r);
for (int num = 1; num <= mx; num++) {
k = max(num - l - 1, 0);
res[num] = max(res[num - 1], num * count[num] + res[k]);
}
return res[mx];
}
int main()
{
int a[] = { 2, 1, 2, 3, 2, 2, 1 }, l = 1, r = 1;
int n = sizeof(a) / sizeof(a[0]);
cout << maxCost(a, n, l, r);
return 0;
}
|
Java
public class GFG {
static int maxCost(int a[], int n, int l, int r)
{
int mx = 0, k;
for (int i = 0; i < n; ++i)
mx = Math.max(mx, a[i]);
int[] count = new int[mx + 1];
for(int i = 0; i < count.length; i++)
count[i] = 0;
for (int i = 0; i < n; i++)
count[a[i]]++;
int[] res = new int[mx + 1];
res[0] = 0;
l = Math.min(l, r);
for (int num = 1; num <= mx; num++) {
k = Math.max(num - l - 1, 0);
res[num] = Math.max(res[num - 1], num * count[num] + res[k]);
}
return res[mx];
}
public static void main(String[] args) {
int a[] = { 2, 1, 2, 3, 2, 2, 1 }, l = 1, r = 1;
int n = a.length;
System.out.println(maxCost(a, n, l, r));
}
}
|
Python 3
def maxCost(a, n, l, r) :
mx = 0
for i in range(n) :
mx = max(mx, a[i])
count = [0] * (mx + 1)
for i in range(n) :
count[a[i]] += 1
res = [0] * (mx + 1)
res[0] = 0
l = min(l, r)
for num in range(1, mx + 1) :
k = max(num - l - 1, 0)
res[num] = max(res[num - 1], num * count[num] + res[k])
return res[mx]
if __name__ == "__main__" :
a = [2, 1, 2, 3, 2, 2, 1 ]
l, r = 1, 1
n = len(a)
print(maxCost(a, n, l, r))
|
C#
using System;
class GFG
{
static int maxCost(int []a, int n,
int l, int r)
{
int mx = 0, k;
for (int i = 0; i < n; ++i)
mx = Math.Max(mx, a[i]);
int[] count = new int[mx + 1];
for(int i = 0; i < count.Length; i++)
count[i] = 0;
for (int i = 0; i < n; i++)
count[a[i]]++;
int[] res = new int[mx + 1];
res[0] = 0;
l = Math.Min(l, r);
for (int num = 1; num <= mx; num++)
{
k = Math.Max(num - l - 1, 0);
res[num] = Math.Max(res[num - 1], num *
count[num] + res[k]);
}
return res[mx];
}
public static void Main()
{
int []a = { 2, 1, 2, 3, 2, 2, 1 };
int l = 1, r = 1;
int n = a.Length;
Console.WriteLine(maxCost(a, n, l, r));
}
}
|
Javascript
<script>
function maxCost(a, n, l, r)
{
var mx = 0, k;
for (var i = 0; i < n; ++i)
mx = Math.max(mx, a[i]);
var count = new Array(mx + 1);
count.fill(0);
for (var i = 0; i < n; i++)
count[a[i]]++;
var res = new Array(mx + 1);
res[0] = 0;
l = Math.min(l, r);
for (var num = 1; num <= mx; num++) {
k = Math.max(num - l - 1, 0);
res[num] = Math.max(res[num - 1],
num * count[num] + res[k]);
}
return res[mx];
}
var a = [ 2, 1, 2, 3, 2, 2, 1 ];
var l = 1, r = 1;
var n = a.length;
document.write(maxCost(a, n, l, r));
</script>
|
Time Complexity: O(max(A))
Auxiliary Space: O(max(A))
Share your thoughts in the comments
Please Login to comment...