Find elements in given Array that are a factor of sum of remaining elements
Last Updated :
10 Feb, 2022
Given an array A[] of size N, the task is to find the elements in the array which are factors of the sum of the remaining element. So just select an element from an array and take the sum of the remaining elements and check whether the sum is perfectly divisible by the selected element or not. If it is divisible then return the element.
Examples:
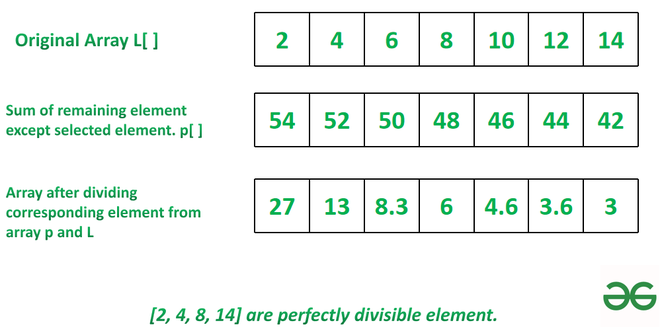
Input: A[] = {2, 4, 6, 8, 10, 12, 14}
Output: [2, 4, 8, 14]
Explanation:
1. Take sum for remaining element except selected one.
2. For element 2, sum of remaining element is 4+6+8+10+12+14=54
3. Similarly for complete array: [54, 52, 50, 48, 46, 44, 42]
3. 54/2, 52/4, 48/8, 42/14 are perfectly divisible so resultant elements are [2, 4, 8, 14]
Input: A[]= {3, 6, 8, 10, 7, 15}
Output: [7]
Naive Approach: Take the sum of all elements from the array. Now subtract each element one by one from sum and append it to new array p[]. Divide each sum by the corresponding index element from a given array and append it to new array q[ ]. Multiply the corresponding element from array A[] and array q[] and compare it with similar indexed elements from array p[]. If they are equal then append it to a new array z[ ]. If no such element is found return -1.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> Factor(vector<int> A)
{
int s = 0;
for (int i = 0; i < A.size(); i++)
{
s += A[i];
}
vector<int> p;
for (int i : A)
p.push_back(s - i);
vector<int> q;
for (int i = 0; i < A.size(); i++)
q.push_back(p[i] / A[i]);
vector<int> z;
for (int i = 0; i < q.size(); i++)
{
if (q[i] * A[i] == p[i])
z.push_back(A[i]);
}
return z;
}
int main()
{
vector<int> A = {2, 4, 6, 8, 10, 12, 14};
vector<int> b = Factor(A);
for (auto i : b)
{
cout << i << " ";
}
}
|
Java
import java.util.ArrayList;
class GFG{
static ArrayList<Integer> Factor(int[] A)
{
int s = 0;
for(int i = 0; i < A.length; i++)
{
s += A[i];
}
ArrayList<Integer> p = new ArrayList<>();
for(int i : A)
p.add(s - i);
ArrayList<Integer> q = new ArrayList<Integer>();
for(int i = 0; i < A.length; i++)
q.add((int) Math.floor(p.get(i) / A[i]));
ArrayList<Integer> z = new ArrayList<Integer>();
for(int i = 0; i < q.size(); i++)
{
if (q.get(i) * A[i] == p.get(i))
z.add(A[i]);
}
if (z.size() == 0)
return new ArrayList<Integer>();
return z;
}
public static void main(String args[])
{
int[] A = { 2, 4, 6, 8, 10, 12, 14 };
ArrayList<Integer> b = Factor(A);
System.out.println(b);
}
}
|
Python3
def Factor(A):
s = sum(A)
p =[]
for i in A:
p.append(s-i)
q =[]
for i in range(len(A)):
q.append(p[i]//A[i])
z =[]
for i in range(len(q)):
if q[i]*A[i]== p[i]:
z.append(A[i])
if len(z)== 0:
return -1
return z
A = [2, 4, 6, 8, 10, 12, 14]
b = Factor(A)
print(b)
|
C#
using System;
using System.Collections.Generic;
public class GFG{
static List<int> Factor(int[] A)
{
int s = 0;
for(int i = 0; i < A.Length; i++)
{
s += A[i];
}
List<int> p = new List<int>();
foreach(int i in A)
p.Add(s - i);
List<int> q = new List<int>();
for(int i = 0; i < A.Length; i++)
q.Add((int) Math.Floor((double)p[i] / A[i]));
List<int> z = new List<int>();
for(int i = 0; i < q.Count; i++)
{
if (q[i] * A[i] == p[i])
z.Add(A[i]);
}
if (z.Count == 0)
return new List<int>();
return z;
}
public static void Main(String []args)
{
int[] A = { 2, 4, 6, 8, 10, 12, 14 };
List<int> b = Factor(A);
foreach(int i in b)
Console.Write(i+", ");
}
}
|
Javascript
<script>
function Factor(A) {
let s = 0;
for (let i = 0; i < A.length; i++) {
s += A[i]
}
p = []
for (i of A)
p.push(s - i)
q = []
for (i = 0; i < A.length; i++)
q.push(Math.floor(p[i] / A[i]))
z = []
for (let i = 0; i < q.length; i++) {
if (q[i] * A[i] == p[i])
z.push(A[i])
}
if (z.length == 0)
return -1
return z
}
A = [2, 4, 6, 8, 10, 12, 14]
b = Factor(A)
document.write(b)
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N)
Efficient Approach: In this approach, there is no need to use multiple loops and multiple arrays. so space complexity and time complexity will be decreased. In this, all the subtraction, division, multiplication operation are performed in a single loop. Follow the steps below to solve the problem:
- Initialize the variable s as the sum of the array A[].
- Initialize the array z[] to store the result.
- Iterate over the range [0, len(A)) using the variables i and perform the following tasks:
- Initialize the variable a as s-l[i], b as a/A[i].
- If b*A[i] equals a then append A[i] into z[].
- After performing the above steps, print -1 if the resultant array is empty, else print the elements of the array z[] as the answer.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int sum(vector<int>& A)
{
int res = 0;
for (auto it : A)
res += it;
return res;
}
vector<int> Factor(vector<int>& A)
{
int s = sum(A);
vector<int> z;
for (int i = 0; i < A.size(); ++i) {
int a = s - A[i];
int b = a / A[i];
if (b * A[i] == a)
z.push_back(A[i]);
}
if (z.size() == 0)
return { -1 };
return z;
}
int main()
{
vector<int> A = { 2, 4, 6, 8, 10, 12, 14 };
vector<int> b = Factor(A);
for (auto it : b)
cout << it << " ";
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int sum(int[] A)
{
int res = 0;
for (int i = 0; i < A.length; i++) {
res += A[i];
}
return res;
}
static ArrayList<Integer> Factor(int[] A)
{
int s = sum(A);
ArrayList<Integer> z = new ArrayList<Integer>();
for (int i = 0; i < A.length; ++i) {
int a = s - A[i];
int b = a / A[i];
if (b * A[i] == a){
z.add(A[i]);
}
}
if (z.size() == 0){
ArrayList<Integer> l1 = new ArrayList<Integer>();
l1.add(-1);
return l1;
}
return z;
}
public static void main (String[] args)
{
int A[] = new int[] { 2, 4, 6, 8, 10, 12, 14 };
ArrayList<Integer> b = Factor(A);
System.out.println(b);
}
}
|
Python3
def Factor(A):
s = sum(A)
z = []
for i in range(len(A)):
a = s-A[i]
b = a//A[i]
if b * A[i] == a:
z.append(A[i])
if len(z) == 0:
return -1
return z
A = [2, 4, 6, 8, 10, 12, 14]
b = Factor(A)
print(b)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int sum(List<int> A)
{
int res = 0;
foreach(int it in A) res += it;
return res;
}
static List<int> Factor(List<int> A)
{
int s = sum(A);
List<int> z = new List<int>();
for (int i = 0; i < A.Count; ++i) {
int a = s - A[i];
int b = a / A[i];
if (b * A[i] == a)
z.Add(A[i]);
}
if (z.Count == 0)
return new List<int>() { -1 };
return z;
}
public static void Main()
{
List<int> A
= new List<int>() { 2, 4, 6, 8, 10, 12, 14 };
List<int> b = Factor(A);
Console.Write("[ ");
int it;
for (it = 0; it < b.Count - 1; it++) {
Console.Write(b[it] + ", ");
}
Console.Write(b[it] + " ]");
}
}
|
Javascript
<script>
function sum(A)
{
var res = 0;
for (var it of A){
res += parseInt(it);}
return res;
}
function Factor(A)
{
var s = sum(A);
var z =[];
for (var i = 0; i < A.length; ++i) {
var a = s - A[i];
var b = parseInt(a / A[i]);
if (b * A[i] == a)
z.push(A[i]);
}
if (z.length == 0)
return [ -1 ];
return z;
}
A = [ 2, 4, 6, 8, 10, 12, 14 ];
b = Factor(A);
for (var it of b)
document.write(it + " ");
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...