Dominant Set of a Graph

In graph theory, a dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is adjacent to at least one member of D. The domination number is the number of vertices in a smallest dominating set for G. 

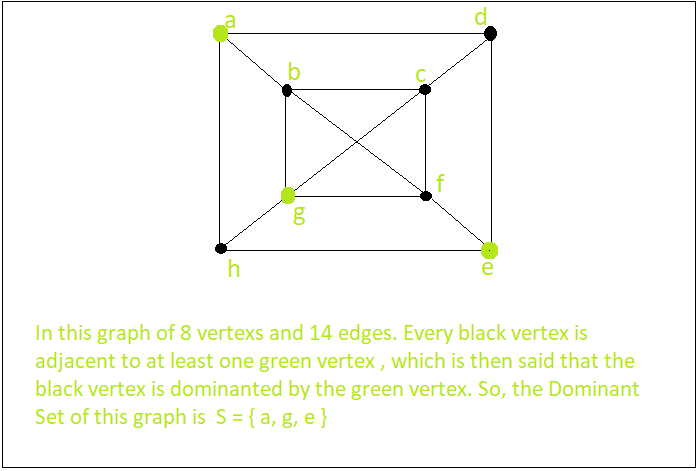
Examples:

Input :   A graph with 4 vertex and 4 edges   
Output :  The Dominant Set S= { a, b } or { a, d } or { a, c } and more.
 
 

Input : A graph with 6 vertex and 7 edges   
Output :  The Dominant Set S= { a, d, f } or { e, c } and more.

It is believed that there may be no efficient algorithm that finds a smallest dominating set for all graphs, but there are efficient approximation algorithms. 

Algorithm :

• First we have to initialize a set ‘S’ as empty
• Take any edge ‘e’ of the graph connecting the vertices ( say A and B )
• Add one vertex between A and B ( let say A ) to our set S
• Delete all the edges in the graph connected to A
• Go back to step 2 and repeat, if some edge is still left in the graph
• The final set S is a Dominant Set of the graph

Implementation:

C++

// C++ program to find the Dominant Set of a graph
#include <bits/stdc++.h>
using namespace std;

vector<vector<int> > g;
bool box[100000];

vector<int> Dominant(int ver, int edge)
{
    vector<int> S; // set S
    for (int i = 0; i < ver; i++) {
        if (!box[i]) {
            S.push_back(i);
            box[i] = true;
            for (int j = 0; j < (int)g[i].size(); j++) {
                if (!box[g[i][j]]) {
                    box[g[i][j]] = true;
                    break;
                }
            }
        }
    }
    return S;
}

// Driver function
int main()
{
    int ver, edge, x, y;

    ver = 5; // Enter number of vertices
    edge = 6; // Enter number of Edges
    g.resize(ver);

    // Setting all index value of an array as 0
    memset(box, 0, sizeof(box));

    // Enter all the end-points of all the Edges
    // g[x--].push_back[y--]      g[y--].push_back[x--]
    g[0].push_back(1);
    g[1].push_back(0); // x = 1, y = 2 ;
    g[1].push_back(2);
    g[2].push_back(1); // x = 2, y = 3 ;
    g[2].push_back(3);
    g[3].push_back(2); // x = 3, y = 4 ;
    g[0].push_back(3);
    g[3].push_back(0); // x = 1, y = 4 ;
    g[3].push_back(4);
    g[4].push_back(3); // x = 4, y = 5 ;
    g[2].push_back(4);
    g[4].push_back(2); // x = 3, y = 5 ;

    vector<int> S = Dominant(ver, edge);
    cout << "The Dominant Set is : { ";
    for (int i = 0; i < (int)S.size(); i++)
        cout << S[i] + 1 << " ";
    cout << "}";
    return 0;
}

Java

// Java program to find the Dominant Set of a graph
import java.util.*;

class GFG
{

static Vector<Integer> []g;
static boolean []box = new boolean[100000];

static Vector<Integer> Dominant(int ver, int edge)
{
    Vector<Integer> S = new Vector<Integer>(); // set S
    for (int i = 0; i < ver; i++)
    {
        if (!box[i])
        {
            S.add(i);
            box[i] = true;
            for (int j = 0; j < (int)g[i].size(); j++)
            {
                if (!box[g[i].get(j)])
                {
                    box[g[i].get(j)] = true;
                    break;
                }
            }
        }
    }
    return S;
}

// Driver code
public static void main(String[] args)
{
    int ver, edge, x, y;

    ver = 5; // Enter number of vertices
    edge = 6; // Enter number of Edges
    g = new Vector[ver];
    for (int i = 0; i < ver; i++)
        g[i] = new Vector<Integer>();


    // Enter all the end-points of all the Edges
    // g[x--].push_back[y--]     g[y--].push_back[x--]
    g[0].add(1);
    g[1].add(0); // x = 1, y = 2 ;
    g[1].add(2);
    g[2].add(1); // x = 2, y = 3 ;
    g[2].add(3);
    g[3].add(2); // x = 3, y = 4 ;
    g[0].add(3);
    g[3].add(0); // x = 1, y = 4 ;
    g[3].add(4);
    g[4].add(3); // x = 4, y = 5 ;
    g[2].add(4);
    g[4].add(2); // x = 3, y = 5 ;

    Vector<Integer> S = Dominant(ver, edge);
    System.out.print("The Dominant Set is : { ");
    for (int i = 0; i < (int)S.size(); i++)
        System.out.print(S.get(i) + 1 + " ");
    System.out.print("}");
}
}

// This code is contributed by Rajput-Ji

Python3

# Python3 code to find the Dominant Set of a graph
from typing import List

g = []
box = []

def Dominant(ver: int, edge: int) -> List[int]:
    S = [] # set S
    for i in range(ver):
        if not box[i]:
            S.append(i)
            box[i] = True
            for j in range(len(g[i])):
                if not box[g[i][j]]:
                    box[g[i][j]] = True
                    break
    return S

# Driver function
if __name__ == '__main__':
    ver = 5 # Enter number of vertices
    edge = 6 # Enter number of Edges
    for i in range(ver):
        g.append([])

    # Setting all index value of an array as False
    box = [False for i in range(ver)]

    # Enter all the end-points of all the Edges
    # g[x].append(y)       g[y].append(x)
    g[0].append(1)
    g[1].append(0) # x = 1, y = 2 ;
    g[1].append(2)
    g[2].append(1) # x = 2, y = 3 ;
    g[2].append(3)
    g[3].append(2) # x = 3, y = 4 ;
    g[0].append(3)
    g[3].append(0) # x = 1, y = 4 ;
    g[3].append(4)
    g[4].append(3) # x = 4, y = 5 ;
    g[2].append(4)
    g[4].append(2) # x = 3, y = 5 ;

    S = Dominant(ver, edge)
    print("The Dominant Set is : {{ {} }}".format(" ".join(str(x+1) for x in S)))

    # This code is contributed by lokeshpotta20.

C#

// C# program to find the Dominant Set of a graph
using System;
using System.Collections.Generic;

class GFG
{

static List<int> []g;
static bool []box = new bool[100000];

static List<int> Dominant(int ver, int edge)
{
    List<int> S = new List<int>(); // set S
    for (int i = 0; i < ver; i++)
    {
        if (!box[i])
        {
            S.Add(i);
            box[i] = true;
            for (int j = 0; j < (int)g[i].Count; j++)
            {
                if (!box[g[i][j]])
                {
                    box[g[i][j]] = true;
                    break;
                }
            }
        }
    }
    return S;
}

// Driver code
public static void Main(String[] args)
{
    int ver, edge;

    ver = 5; // Enter number of vertices
    edge = 6; // Enter number of Edges
    g = new List<int>[ver];
    for (int i = 0; i < ver; i++)
        g[i] = new List<int>();

    // Enter all the end-points of all the Edges
    // g[x--].push_back[y--]     g[y--].push_back[x--]
    g[0].Add(1);
    g[1].Add(0); // x = 1, y = 2 ;
    g[1].Add(2);
    g[2].Add(1); // x = 2, y = 3 ;
    g[2].Add(3);
    g[3].Add(2); // x = 3, y = 4 ;
    g[0].Add(3);
    g[3].Add(0); // x = 1, y = 4 ;
    g[3].Add(4);
    g[4].Add(3); // x = 4, y = 5 ;
    g[2].Add(4);
    g[4].Add(2); // x = 3, y = 5 ;

    List<int> S = Dominant(ver, edge);
    Console.Write("The Dominant Set is : { ");
    for (int i = 0; i < (int)S.Count; i++)
        Console.Write(S[i] + 1 + " ");
    Console.Write("}");
}
}

// This code is contributed by PrinciRaj1992

Output

The Dominant Set is : { 1 3 5 }