Cubic Function

Cube Function or Cubic Function, is a polynomial function of the form ax³ + bx² + cx + d where a, b, c and d are real numbers and a ≠ 0. Cubic functions have either one or three real roots and always have at least one real root due to their odd-degree nature.

In this article, we will explore more about the cubic function, including its domain and range, asymptotes, intercepts, critical & inflection points, as well as its graph. We will also solve some examples of cubic functions.

What is Cubic Function?

Any polynomial function with degree 3 is called cubic function. Alternatively, the function of the form ax³ + bx² + cx + d is referred to as cubic function. Here, a, b, c and d are real numbers and a ≠ 0.

Standard Form of Cubic Function is ax³ + bx² + cx + d.

Where a, b, c and d are real numbers and a ≠ 0.

Note: The fundamental cubic function is f(p) = p³.

Domain and Range of Cubic Function

The cubic function y = f(x) is defined for set of all real numbers for x. So, the domain of the cubic function is set of all real numbers. The value of y obtained also covers the set of all real numbers. So, the range of the cubic function is set of all real numbers.

• Domain: (−∞,∞) or R
• Range: (−∞,∞) or R

Read More about Domain and Range of Function.

Asymptotes of Cube Function

Asymptotes are referred to as the values that are not in the domain and range. The domain and range of the cubic function includes the set of all real numbers which implies that there is no asymptote for cubic functions. So, the cubic function does not have a vertical asymptote or horizontal asymptote.

Read More about Asymptotes.

Roots of Cubic Function

Roots of a cubic function, also known as its zeros or x-intercepts, are the values of x where the function f(x) equals zero.

The general form of a cubic function is ax³ + bx² + cx + d, where a, b, c, and d are constants, and a is not equal to zero.

We can learn more about Roots in the article of Zeros of Polynomial.

Factors of Cubic Function

Factors are those expressions which can divide the cubic function exactly without leaving any remainder.

If m, n and o are the root of cubic function then cubic function can be written as:

a(x – m)(x – n)(x – o) = 0

Where a is the leading coefficient.

Read More about Factorization of Polynomial.

Intercepts of a Cubic Function

The intercepts of a cubic function are the points where the graph of the function intersects the x-axis and the y-axis. There can be two intercepts for any function based on the intersection with axis i.e.,

• x-intercept
• y-intercept

X-Intercept

The x-intercept of cubic function is obtained by solving the function by putting f(x) = 0. We know that the degree of the cubic function is 3 so, there are maximum 3 roots of the cubic function.

Thus, there can be maximum of three x-intercept for any cubic function.

Y-Intercept

The y-intercept of cubic function is obtained by solving the function by putting x = 0 and determining the value of f(x) [i.e., y]. There is exactly one y-intercept for a cubic function.

For example, consider the cubic function f(x)= ax³ + bx² + cx + d.

• To find the x-intercepts, set f(x) = 0 and solve the cubic equation ax³ + bx² + cx + d = 0 for x.
• To find the y-intercept, substitute x = 0 into the function f(x) to get f(0) i.e., d.

Read More about X and Y Intercepts.

Graph of Cubic Function

A cubic function is typically represented by the equation ax³ + bx² + cx + d., where a, b, c, and d are constants. Depending on the specific values of these constants, the graph of a cubic function can take various shapes. Graph of the cubic function exhibits S shape like graph.

Graph of fundamental cubic function i.e., f(x) = x³ is given as follows:

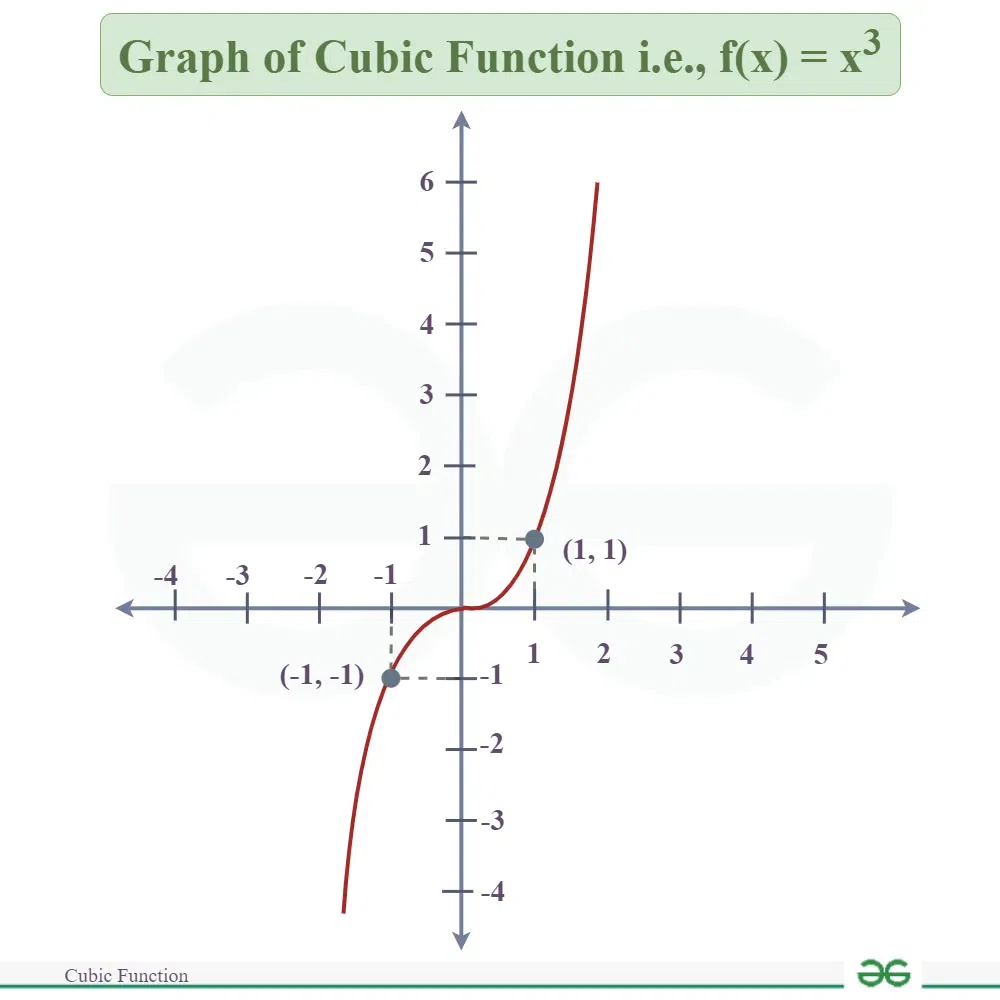
Read More about Graph of Polynomial.

Characteristics of Cubic Function

There are multiple characteristics of a cubic function some of these are listed below:

• A cubic function has degree 3.
• It can have one or three real roots.
• It can have zero or two complex roots.
• It has only one inflection point.
• A cubic function can have two critical points local maxima and local minima.
• Cubic functions may exhibit symmetry depending on the coefficients.
  • They can be odd functions (symmetric about the origin) if b = 0
  • They can be even functions (symmetric about the y-axis) if c=0.

Inverse of Cubic Function

Steps to find the inverse of the cubic function are:

• First write cubic function as y = f(x).
• Then replace a by y and y by x.
• Then, get the cubic degree one side and all the other terms other side and take cube root.
• The obtained value of y is the inverse of cubic function.

Inverse of cube function is cube root function i.e., for f(x) = x³,

f^-1(x) = ∛x

Example: Find the inverse of cubic function f(x) = x³ + 2.

Solution:

Let y = f(x) = x³ + 2

Now, replace y by x and x by y

x = y³ + 2

⇒ y³ = x – 2

⇒ y = ∛(x – 2)

Since y = f^-1(x)

f^-1(x) = ∛(x – 2)

So, the inverse of given cubic function is ∛(x – 2).

Read more about Cube Root Function.

Extrema of Cubic Function

Extrema refers to the maximum or minimum value of a function within a given interval or over its entire domain. For any polynomial function of degree n there can be at most n – 1 extrema.

Note: If the cubic function is always increasing or always decreasing over its entire domain, it does not have any local extrema.

To find extrema of any function we need to find critical points and inflection points for some cases as well. Let’s discuss both in detail with the help of some examples as well.

Critical Points of Cubic Function

The critical point is referred to as the point where the function has its minimum or maximum value. In other words, the point where the function changes its behavior from increasing to decreasing or vice-versa then, the point is called as critical point of the function. To find the critical points of cubic function we equate the first order derivative of the function with zero and then solve the resultant equation.

For example, consider the cubic function f (x) = ax³ + bx² + cx + d.

• To find the critical point of the above function we determine f'(x) i.e., f'(x) = 3ax² + 2bx + c
• Now, equate f'(x) = 0 i.e., 3ax² + 2bx + c = 0
• Solve for x.
• The values of x are the critical points of above cubic equation.

Inflection Points of Cubic Function

The inflection points are referred to as the points where the function curve changes from concave up to concave down or vice-versa. To find the inflection points of the cubic function we equate the second order derivative of the cubic function with zero and solve.

For example, consider the cubic function f (x) = ax³ + bx² + cx + d.

• To find the inflection point of the above function we determine f”(x) i.e., f”(x) = 6ax + 2b
• Now, equate f”(x) = 0 i.e., 6ax+ 2b = 0
• Solve for x we get x = -2b/ 6a
• The value of x = -b /3a is the inflection point of above cubic equation.

End Behavior of Cube Function

We know that the cubic function is of the form ax³ + bx² + cx + d where ‘a’ is called as the leading coefficient. Based on the leading coefficient we can obtain the end behavior of the cube function. There are two cases for the end behavior of the cubic function.

• When Leading Coefficient is Positive
• When Leading Coefficient is Negative

When Leading Coefficient is Positive

When the leading coefficient is positive i.e., a > 0 then, the cubic function depicts the following behavior.

f(x) → ∞ as x→∞ and f(x) → -∞ as x→-∞.

When Leading Coefficient is Negative

When the leading coefficient is negative i.e., a < 0 then, the cubic function depicts the following behavior.

f(x)→-∞ as x→∞ and f(x)→∞ as x→-∞

Cubic Function Vs Quadratic Function

The key differences between cubic and quadratic function are:

Aspect	Quadratic Function	Cubic Function
Degree of the Polynomial	2 (quadratic)	3 (cubic)
General Form	ax2 + bx + c	ax3 + bx2 + cx + d
Number of Roots	Maximum of 2 real roots	Maximum of 3 real roots
Shape of Graph	Parabola	Skewed “S” shape
Turning Points	1 (minimum or maximum)	Up to 2 (local extrema)
Behavior at Extremes	Continues to infinity	May turn or flatten at extremes

Read More,

• Solving Cubic Equations
• Relationship between Zeroes and Coefficients of a Polynomial
• Quadratic Function

Solved Examples on Cubic Functions

Example 1:Find the x-intercept of the cubic function f(x) = (x + 1)(x – 2)(x + 7).

Solution:

To find x-intercept of the cubic function we put f(x) = 0

f(x) = (x + 1)(x – 2)(x + 7)

⇒ (x + 1)(x – 2)(x + 7) = 0

⇒ (x + 1) = 0 ⇒ x = -1

⇒ (x – 2) = 0 ⇒ x = 2

⇒ (x + 7) = 0 ⇒ x = -7

So, the x-intercepts of the given cubic function are -1, 2 and -7.

Example 2: Find the y-intercept of the cubic function y = x³ + x² + 5x – 10.

Solution:

To find y-intercept of the cubic function y = x³ + x² + 5x – 10 we put x = 0.

y = x³ + x² + 5x – 10

⇒ y = 0³ + 0² + 5(0) – 10

⇒ y = -10

The y-intercept of the given cubic function is -10.

Example 3:Find the critical points of the cubic function y = 4x³ + 5x² + 3x + 2.

Solution:

To find the critical points we find the first order derivative of y and equate it to 0.

y’ = 12x² + 10x + 3

⇒ 12x² + 10x + 3 = 0

⇒ x = (-5 + √11i) / 12 and (-5 – √11i) / 12

The critical points of given cubic function are (-5 + √11i) / 12 and (-5 – √11i) / 12.

Example 4:Find the inflection point of the cubic function f(x) = x³ + 2x² + 3x + 5.

Solution:

To find inflection point find second derivative of f(x) and equate to 0 and solve.

f'(x) = 3x² + 4x + 3

⇒ f”(x) = 6x + 4

⇒ 6x + 4 = 0

⇒ x = -4 / 6

The inflection point of the given cubic function is – 4 / 6.

Practice Questions on Cube Function

Q1: Find the x-intercept of the cubic function x (x – 4)(x + 5).

Q2: Find the y-intercept of the cubic function y = x³ + 2x² + 9x – 15.

Q3: Find the critical points of the cubic function y = 4x³ + 5x² + 3x + 2.

Q4: Find the inflection point of the cubic function f(x) = x³ + 10x² + 2x + 3.

FAQs on Cubic Function

What is Cube Function?

A polynomial function with degree 3 is called cube function.

What is the Degree of Cubic Function?

The degree of a cubic function is 3.

How can we Solve Cubic Function?

To solve any cubic equation we can use following steps:

• Start with the cubic function f(x) = ax³ + bx² + cx + d.
• Set the function equal to zero: f(x) = 0.
• Use one of the following methods to find the roots:
  • Factorization if possible.
  • Graphical methods: identify x-intercepts.
  • Numerical methods like Newton’s method.
  • The cubic formula (though rarely used due to complexity).
• Check for complex roots if necessary.
• Verify solutions by plugging them back into the original equation.
• Express solutions in the desired form (e.g., decimal approximation or exact form).

How to Factor a Cubic Function?

There are various methods to factorize a cubic function, some of these methods are:

• Rational Root Theorem
• Grouping
• Sum/Difference of Cubes
• Trial and Error

What is the Standard Equation of Cubic Function?

The standard equation of cubic function is:

ax³ + bx² + cx + d

where a, b, c and d are real numbers and a ≠ 0

How Many Real Roots a Cubic Function Can Have?

A cubic function can have one or three real roots.

How Many Complex Roots a Cubic Function Can Have?

A cubic function can have zero or two complex roots.

How to Find the Intercepts of Cubic Function?

To find x-intercept we put f(x) = 0 and solve for x. To find y-intercept we put x = 0 and solve for f(x).