Count ways to distribute exactly one coin to each worker
Last Updated :
25 Jun, 2021
Given two arrays coins[] and salaries[] where coins[i] represents the value of ith coin and salaries[j] represents the minimum value of the coin that jth worker will accept. The task is to compute the number of ways to distribute exactly one coin to each worker. Since the answer can be large, print it modulo 109 + 7.
Examples:
Input: coins[] = {1, 2, 3}, salaries[] = {1, 2}
Output: 4
Explanation:
If the coin with value 1 is not used, then the remaining two coins are acceptable by both workers, contributing two possible ways to pay the workers.
If the coin with value 1 is used, then it can only be used for the first worker. Then either of the remaining coins can be used to pay the second worker. This also contributes to two possible ways.
Therefore, the four ways to pay the two workers are [2, 3], [3, 2], [1, 2], [1, 3].
Input: coins[] = {1, 2}, salaries[] = {2}
Output: 1
Approach: The idea is to use the Sorting and Two Pointers technique to solve the problem. Follow the steps below to solve the problem:
- Sort the salaries in descending order.
- Let f(i) be the number of coins used to pay the ith worker in the absence of any other workers. Since the salary[] array is sorted so the first worker demands the highest salary and the last worker demands the lowest salary. Therefore, the result is:
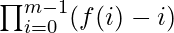
- For the function f(i), i is equal to the number of coins that are available to use to pay the current worker assuming that all previous workers have been paid.
- As the workers are sorted in non-increasing order of salaries, so any coin used to pay a former worker is guaranteed to be usable to pay the current worker. So the number of coins that can be used to pay the current worker will always be equal to f(i) ? i, independent of the previous choices made.
- To compute f(i) efficiently, use two pointers to track the number of coins that are currently valid.
- Print the total count of ways after all the above steps.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int MOD = 1000000007;
int solve(vector<int>& values,
vector<int>& salary)
{
long long ret = 1;
int amt = 0;
sort(values.begin(), values.end());
sort(salary.begin(), salary.end());
while (salary.size()) {
while (values.size()
&& values.back()
>= salary.back()) {
amt++;
values.pop_back();
}
if (amt == 0)
return 0;
ret *= amt--;
ret %= MOD;
salary.pop_back();
}
return ret;
}
int main()
{
vector<int> values{ 1, 2 }, salary{ 2 };
cout << solve(values, salary);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int MOD = 1000000007;
static int solve(Vector<Integer> values,
Vector<Integer> salary)
{
int ret = 1;
int amt = 0;
Collections.sort(values);
Collections.sort(salary);
while (salary.size() > 0)
{
while (values.size() > 0 &&
values.get(values.size() - 1) >=
salary.get(salary.size() - 1))
{
amt++;
values.remove(values.size() - 1);
}
if (amt == 0)
return 0;
ret *= amt--;
ret %= MOD;
salary.remove(salary.size() - 1);
}
return ret;
}
public static void main(String[] args)
{
Vector<Integer> values = new Vector<Integer>();
values.add(1);
values.add(2);
Vector<Integer> salary = new Vector<Integer>();
salary.add(2);
System.out.print(solve(values, salary));
}
}
|
Python3
MOD = 1000000007
def solve(values, salary):
ret = 1
amt = 0
values = sorted(values)
salary = sorted(salary)
while (len(salary) > 0):
while ((len(values) and
values[-1] >= salary[-1])):
amt += 1
del values[-1]
if (amt == 0):
return 0
ret *= amt
amt -= 1
ret %= MOD
del salary[-1]
return ret
if __name__ == '__main__':
values = [ 1, 2 ]
salary = [2]
print(solve(values, salary))
|
C#
using System;
using System.Collections;
class GFG{
static int MOD = 1000000007;
static int solve(ArrayList values,
ArrayList salary)
{
int ret = 1;
int amt = 0;
values.Sort();
salary.Sort();
while (salary.Count > 0)
{
while (values.Count > 0 &&
(int)values[values.Count - 1] >=
(int)salary[salary.Count - 1])
{
amt++;
values.RemoveAt(values.Count - 1);
}
if (amt == 0)
return 0;
ret *= amt--;
ret %= MOD;
salary.RemoveAt(salary.Count - 1);
}
return ret;
}
public static void Main(string[] args)
{
ArrayList values = new ArrayList();
values.Add(1);
values.Add(2);
ArrayList salary = new ArrayList();
salary.Add(2);
Console.Write(solve(values, salary));
}
}
|
Javascript
<script>
var MOD = 1000000007;
function solve(values, salary)
{
var ret = 1;
var amt = 0;
values.sort((a,b)=>a-b);
salary.sort((a,b)=>a-b);
while (salary.length) {
while (values.length
&& values[values.length-1]
>= salary[salary.length-1]) {
amt++;
values.pop();
}
if (amt == 0)
return 0;
ret *= amt--;
ret %= MOD;
salary.pop();
}
return ret;
}
var values = [1, 2 ], salary = [2];
document.write( solve(values, salary));
</script>
|
Time Complexity: O(N*log N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...