Cholesky Decomposition

Cholesky Decomposition is one of the types of many decompositions in linear algebra which is a branch of mathematics that deals with linear equations and vectors. Decomposition is the term related to the factorization of matrices in linear algebra, and Cholesky is one of the ways to factorize or decompose the matrix into two matrices. This article explores the Cholesky Decomposition in detail including its definition, steps to factorize matrices using Cholesky Decomposition, and some of the solved examples. So, let’s start learning about this exciting topic of Cholesky Decomposition.

What is Cholesky Decomposition?

Cholesky Decomposition is the decomposition of Hermitian, positive definite matrix into the multiplication of two matrices, where one is a positive diagonal lower triangular matrix and the other is its conjugate transpose matrix i.e., upper triangular matrix. As Cholesky decomposition can represent matrices as a product of two matrices, it is also called Cholesky Factorization.

The Cholesky decomposition is specially defined for symmetric matrices and Cholesky Decomposition is used widely as it is faster than the LU decomposition. Let A be any Hermitian, positive definite matrix, then the Cholesky decomposition can be given by:

A = LL*

Where,

• L is the lower triangular matrix of A with a positive diagonal
• L* is the conjugate transpose matrix of A

Note: Every Hermitian positive definite matrix has a unique Cholesky decomposition.

How to Evaluate Cholesky Decomposition?

To decompose a matrix X using Cholesky decomposition we first decompose the matrix A in the form A = LL* where L is assumed to be a positive diagonal lower triangular matrix and L* is the conjugate transpose of L. Then, we have to find the elements of L. To find the value of the diagonal elements we use the formula

L_vv = √(A_vv – ∑_u<v L_vu (L_vu)*)

And to find the value of non-diagonal elements we use the formula

L_tv = (1 / L_vv)(A_tv – ∑_u<v L_tu (L_vu)*)

After finding all the elements arrange them in the lower triangular matrix L and then find L* which is the conjugate transpose of L. Finally, evaluate the product of LL* to get the simplified matrix of A.

Steps for Cholesky Decomposition

To decompose or factorize any Hermitian symmetric matrix, we can use the following steps:

Step 1: First write the given matrix in the decomposed form.

Let A be the positive definite symmetric matrix which can be decomposed as A = LL^*.

Step 2: Now, we have to evaluate matrix L where L is defined as:

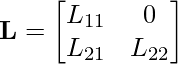
Step 3: To evaluate the diagonal element, use the formula:

L_vv = √(A_vv – ∑_u<v L_vu (L_vu)*)

Where L* is the conjugate of L.

Step 4: To evaluate the non-diagonal element, use the formula:

L_tv = (1 / L_vv)(A_tv – ∑_u<v L_tu (L_vu)*)

Where L* is the conjugate of L.

Step 5: Put all the elements in L and evaluate A = LL^*.

Example: Find the Cholesky decomposition for a matrix A =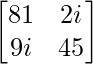

Solution:

A =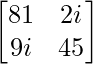

According to Cholesky decomposition the matrix can be written as:

A = LL*

where L is the lower triangular matrix of A and L* is the conjugate transpose matrix of L.

First, we have to find the lower triangular matrix of A.

Let the lower triangular matrix for P be L =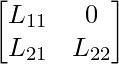

We calculate the elements of lower triangular matrix using the following formulas:

The diagonal element of L is calculated using:

L_vv = √(A_vv – ∑_u<v L_vu (L_vu)*)

The non-diagonal element is calculated using formula:

L_tv = (1 / L_vv)(A_tv – ∑_u<v L_tu (L_vu)*)

L₁₁ = √(A₁₁ – ∑_u<1 L_1u (L_1u)*) [Since, there is no value u which is lesser than 1(here, v=1) so, ∑_u<v L_vu (L_vu)*= 0 ]

⇒ L11 = √(81 – 0) = √81 = 9

L₂₁ = (1 / L₁₁)(A₂₁ )

⇒ L₂₁ = (1 / 9)(9i) = i

(L₂₁)* = -i (conjugate of i)

L22 = Ltv = (1 / Lvv)(Atv – ∑u<v Ltu (Lvu)*)

(∑_u<v L_tu (L_vu)* is the summation of the values of L where u<v)

L₂₂ = √(A₂₂ – ∑_u<2 L₂₁ (L₂₁)*) Here, v = 2 so u should be the values less than 2. By putting values in formula)

⇒ L₂₂ = √(A₂₂ – L₂₁ (L₂₁)*)

⇒ L₂₂ = √(45 – (-i) (i))

⇒ L₂₂ = √(45 + i²)

⇒ L₂₂ = √(45 – 1) [i² = -1]

⇒ L₂₂ = √44

The lower triangular matrix of P according to Cholesky decomposition is:

L =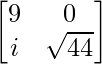

Now, we will find L* i.e., conjugate transpose of L

L* =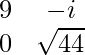

Finally, we apply

A = LL*

A =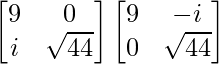

The final matrix A after applying Cholesky decomposition is:

A =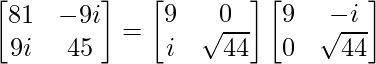

Application of Cholesky Decomposition

Some applications of Cholesky decomposition of the positive definite symmetric matrix are:

• It is used to solve the systems of linear equations.
• It can be used to compute the inverse of the matrix.
• Cholesky decomposition is widely used in Monte Carlo stimulation.

Cholesky Decomposition Examples

Example 1: Find the Cholesky decomposition for a matrix X whose lower triangular matrix is given by: L =

Solution:

The lower triangular matrix is given:

L =

The conjugate transpose of the above lower triangular matrix is:

L* =

From Cholesky decomposition X can be written as:

X = L L*

X =

X =

Example 2: Find the lower triangular matrix using Cholesky decomposition for a matrix A =

Solution:

Let the lower triangular matrix for A be L =

The diagonal element of L is calculated using:

L_vv = √(A_vv – ∑_u<v L_vu (L_vu)*)

The non-diagonal element is calculated using formula:

L_tv = (1 / L_vv)(A_tv – ∑_u<v L_tu (L_vu)*)

L₁₁ = √(A₁₁ – ∑_u<1 L_1u (L_1u)*) [∑_u<1 L_1u (L_1u)* = 0 as v = 1 is the least value and there is no u lesser than v]

⇒ L₁₁ = √(36 – 0)

⇒ L₁₁ = 6

L₂₁ = (1 / L₁₁)(A₂₁ – ∑_u<1 L_2u (L_1u)*)

[Here, there is no u which is lesser than 1 so, ∑_u<1 L_2u (L_1u)* = 0]

⇒ L₂₁ = (1 / L₁₁)(A₂₁ – 0)

⇒ L₂₁ = (1 / 6)(-12i) = -2i

Thus, (L₂₁)* = 2i

L₂₂ = √(A₂₂ – ∑_u<2 L₂₁ (L₂₁)*) [Here, only u = 1 is the value satisfying the condition u < 2. Putting the values in the formula]

⇒ L₂₂ = √(A₂₂ – L₂₁ (L₂₁)*)

⇒ L₂₂ = √(42 – (-2i) (2i))

⇒ L₂₂ = √(42 + 4i²)

⇒ L₂₂ = √(42 – 4) [i² = -1]

⇒ L₂₂ = √38

The lower triangular matrix of A according to Cholesky decomposition is:

L =

Example 3: Find the Cholesky decomposition for a matrix X whose lower triangular matrix is given by: L =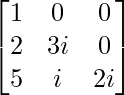

Solution:

The lower triangular matrix is given:

L =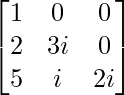

The conjugate transpose of the above lower triangular matrix is:

L* =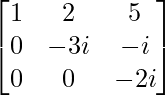

From Cholesky decomposition X can be written as:

X = L L*

X =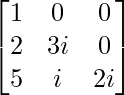[Tex] \begin {bmatrix} 1&2&5\\ 0& -3i&-i\\ 0& 0 &-2i \end{bmatrix} [/Tex]

X =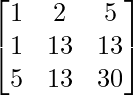

Practise Problems on Cholesky Decomposition

• Problem 1: Compute the Cholesky decomposition of the following matrix:

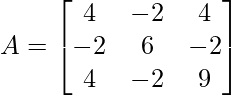
• Problem 2: Perform Cholesky decomposition on the matrix A given below

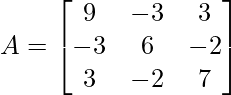
• Problem 3: Calculate the Cholesky Decomposition for given positive definite matrix:

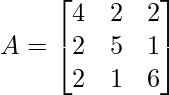
FAQs on Cholesky Decomposition

1. What is Cholesky Decomposition?

The decomposition of the symmetric positive definite matrix into the lower triangular matrix with positive diagonal and its conjugate transpose is called the Cholesky decomposition.

2. Write the Other Name of Cholesky Decomposition?

The other name of Cholesky decomposition is Cholesky Factorization.

3. What is the Formula for Cholesky Decomposition?

Given a Hermitian, positive definite matrix A, its Cholesky Decomposition is represented as A = LL*, where L is the lower triangular matrix and L* is its conjugate transpose.

4. What are the Conditions for Cholesky Decomposition to Exist?

Cholesky Decomposition exists if the matrix is both Hermitian (symmetric in the real case) and positive definite.

5. Can Cholesky Decomposition be used for Non-Positive Definite Matrices?

No, Cholesky Decomposition requires the matrix to be positive definite. If the matrix is not positive definite, the decomposition cannot be performed.

6. Is Cholesky Decomposition faster than LU decomposition?

Yes, the Cholesky decomposition is faster than LU decomposition as it more computationaly efficient.

7. List Some Applications of Cholesky Decomposition.

Some of the applications of the Cholesky decomposition include solving the system of equations in linear algebra, computing inverse of the matrix etc.