Check if a number is divisible by 23 or not
Last Updated :
31 Jul, 2022
Given a number, the task is to quickly check if the number is divisible by 23 or not.
Examples:
Input : x = 46
Output : Yes
Input : 47
Output : No
A solution to the problem is to extract the last digit and add 7 times of last digit to remaining number and repeat this process until a two digit number is obtained. If the obtained two digit number is divisible by 23, then the given number is divisible by 23.
Approach:
- Extract the last digit of the number/truncated number every time
- Add 7*(last digit of the previous number) to the truncated number
- Repeat the above three steps as long as necessary.
Illustration:
17043-->1704+7*3
= 1725-->172+7*5
= 207 which is 9*23,
so 17043 is also divisible by 23.
Mathematical Proof :
Let 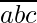 be any number such that
be any number such that 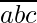 =100a+10b+c .
=100a+10b+c .
Now assume that 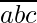 is divisible by 23. Then
is divisible by 23. Then
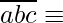 0 (mod 23)
0 (mod 23)
100a+10b+c 0 (mod 23)
0 (mod 23)
10(10a+b)+c 0 (mod 23)
0 (mod 23)
10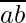 +c
+c 0 (mod 23)
0 (mod 23)
Now that we have separated the last digit from the number, we have to find a way to use it.
Make the coefficient of 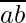 1.
1.
In other words, we have to find an integer such that n such that 10n 1 mod 23.
1 mod 23.
It can be observed that the smallest n which satisfies this property is 7 as 70 1 mod 23.
1 mod 23.
Now we can multiply the original equation 10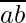 +c
+c 0 (mod 23)
0 (mod 23)
by 7 and simplify it:
70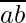 +7c
+7c 0 (mod 23)
0 (mod 23)
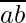 +7c
+7c 0 (mod 23)
0 (mod 23)
We have found out that if 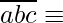 0 (mod 23) then,
0 (mod 23) then,
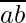 +7c
+7c 0 (mod 23).
0 (mod 23).
In other words, to check if a 3-digit number is divisible by 23,
we can just remove the last digit, multiply it by 7,
and then subtract it from the rest of the two digits.
C++
#include <iostream>
using namespace std;
bool isDivisible(long long int n)
{
while (n / 100)
{
int d = n % 10;
n /= 10;
n += d * 7;
}
return (n % 23 == 0);
}
int main()
{
long long int n = 1191216;
if (isDivisible(n))
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
class GFG
{
static boolean isDivisible(long n)
{
while (n / 100 != 0)
{
long d = n % 10;
n /= 10;
n += d * 7;
}
return (n % 23 == 0);
}
public static void main(String[] args)
{
long n = 1191216;
if(isDivisible(n))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python 3
def isDivisible(n) :
while n // 100 :
d = n % 10
n //= 10
n += d * 7
return (n % 23 == 0)
if __name__ == "__main__" :
n = 1191216
if (isDivisible(n)) :
print("Yes")
else :
print("No")
|
C#
class GFG
{
static bool isDivisible(long n)
{
while (n / 100 != 0)
{
long d = n % 10;
n /= 10;
n += d * 7;
}
return (n % 23 == 0);
}
public static void Main()
{
long n = 1191216;
if(isDivisible(n))
System.Console.WriteLine("Yes");
else
System.Console.WriteLine("No");
}
}
|
PHP
<?php
function isDivisible($n)
{
while (intval($n / 100))
{
$n = intval($n);
$d = $n % 10;
$n /= 10;
$n += $d * 7;
}
return ($n % 23 == 0);
}
$n = 1191216;
if (isDivisible($n))
echo "Yes" . "\n";
else
echo "No" . "\n";
?>
|
Javascript
<script>
function isDivisible(n)
{
while (Math.floor(n / 100) != 0)
{
let d = n % 10;
n = Math.floor(n/10);
n += d * 7;
}
return (n % 23 == 0);
}
let n = 1191216;
if(isDivisible(n))
document.write("Yes");
else
document.write("No");
</script>
|
Time Complexity: O(log10N)
Auxiliary Space: O(1)
Note that the above program may not make a lot of sense as could simply do n % 23 to check for divisibility. The idea of this program is to validate the concept. Also, this might be an efficient approach if input number is large and given as string.
Share your thoughts in the comments
Please Login to comment...