Find permutation of n which is divisible by 3 but not divisible by 6

Given an integer 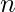. The task is to find another integer which is permutation of n, divisible by 3 but not divisible by 6. Given that n is divisible by 6. If no such permutation is possible print -1.

Examples:  

Input: n = 336
Output: 363

Input: n = 48
Output: -1

For a number to be divisible by 6, it must be divisible by 3 as well as 2, means every even integer divisible by 3 is divisible by 6. So, an integer which is divisible by 3 but not 6 is odd integer divisible by 3.
So, if integer n contains any odd integer then there exists a permutation which is divisible by 3 but not 6, else no such permutation exist.

Algorithm:

1. let LEN is length of integer (i.e. ceil(log10(n))).
2. iterate over LEN and check whether n is even or odd.
   • if n is odd return n
   • else right – rotate n once. and continue.
3. if LEN is over return -1

Below is the implementation of the above approach: 

C++

// C++ program to find permutation of n
// which is divisible by 3 but not
// divisible by 6

#include <bits/stdc++.h>
using namespace std;

// Function to find the permutation
int findPermutation(int n)
{
    // length of integer
    int len = ceil(log10(n));

    for (int i = 0; i < len; i++) {
        // if integer is even
        if (n % 2 != 0) {
            // return odd integer
            return n;
        }
        else {
            // rotate integer
            n = (n / 10) + (n % 10) * pow(10, len - i - 1);
            continue;
        }
    }

    // return -1 in case no required
    // permutation exists
    return -1;
}

// Driver Code
int main()
{
    int n = 132;

    cout << findPermutation(n);

    return 0;
}

Java

// Java program to find permutation
// of n which is divisible by 3
// but not divisible by 6
import java.lang.*;
import java.util.*;

class GFG
{
// Function to find the permutation
static int findPermutation(int n)
{
    // length of integer
    int len = (int)Math.ceil(Math.log10(n));

    for (int i = 0; i < len; i++)
    {
        // if integer is even
        if (n % 2 != 0)
        {
            // return odd integer
            return n;
        }
        else
        {
            // rotate integer
            n = (n / 10) + (n % 10) *
                (int)Math.pow(10, len - i - 1);
            continue;
        }
    }

    // return -1 in case no required
    // permutation exists
    return -1;
}

// Driver Code
public static void main(String args[])
{
    int n = 132;

    System.out.println(findPermutation(n));
}
}

// This code is contributed
// by Akanksha Rai(Abby_akku)

Python3

# Python3 program to find permutation
# of n which is divisible by 3 but
# not divisible by 6
from math import log10, ceil, pow

# Function to find the permutation
def findPermutation(n):

    # length of integer
    len = ceil(log10(n))

    for i in range(0, len, 1):

        # if integer is even
        if n % 2 != 0:

            # return odd integer
            return n
        else:

            # rotate integer
            n = ((n / 10) + (n % 10) *
                  pow(10, len - i - 1))
            continue

    # return -1 in case no required
    # permutation exists
    return -1

# Driver Code
if __name__ == '__main__':
    n = 132

    print(int(findPermutation(n)))

# This code is contributed
# by Surendra_Gangwar

C#

// C# program to find permutation
// of n which is divisible by 3
// but not divisible by 6
using System;

class GFG
{
// Function to find the permutation
static int findPermutation(int n)
{
    // length of integer
    int len = (int)Math.Ceiling(Math.Log10(n));

    for (int i = 0; i < len; i++)
    {
        // if integer is even
        if (n % 2 != 0)
        {
            // return odd integer
            return n;
        }
        else
        {
            // rotate integer
            n = (n / 10) + (n % 10) *
                (int)Math.Pow(10, len - i - 1);
            continue;
        }
    }

    // return -1 in case no required
    // permutation exists
    return -1;
}

// Driver Code
public static void Main()
{
    int n = 132;

    Console.WriteLine(findPermutation(n));
}
}

// This code is contributed
// by Akanksha Rai(Abby_akku)

PHP

<?php
// PHP program to find permutation
// of n which is divisible by 3 but
// not divisible by 6

// Function to find the permutation
function findPermutation($n)
{
    // length of integer
    $len = ceil(log10($n));

    for ($i = 0; $i < $len; $i++)
    {
        // if integer is even
        if ($n % 2 != 0)
        {
            // return odd integer
            return (int)$n;
        }
        else
        {
            // rotate integer
            $n = ($n / 10) + ($n % 10) *
                  pow(10, $len - $i - 1);
            continue;
        }
    }

    // return -1 in case no required
    // permutation exists
    return -1;
}

// Driver Code
$n = 132;

echo findPermutation($n);

// This code is contributed by mits
?>

Javascript

<script>
// java script  program to find permutation
// of n which is divisible by 3 but
// not divisible by 6

// Function to find the permutation
function findPermutation(n)
{

    // length of integer
    let len = Math.ceil(Math.log10(n));

    for (let i = 0; i < len; i++)
    {

        // if integer is even
        if (n % 2 != 0)
        {

            // return odd integer
            return parseInt(n);
        }
        else
        {

            // rotate integer
            n = (n / 10) + (n % 10) *
                Math.pow(10, len - i - 1);
            continue;
        }
    }

    // return -1 in case no required
    // permutation exists
    return -1;
}

// Driver Code
let n = 132;

document.write( findPermutation(n));

// This code is contributed by sravan kumar (vignan)
</script>

Output:

213

Time complexity: O(logn) for given input number n

Auxiliary space: O(1)