Bubble Sort algorithm using JavaScript

Bubble sort algorithm is an algorithm that sorts the array by comparing two adjacent elements and swaps them if they are not in the intended order. Here order can be anything like increasing order or decreasing order.

How Bubble-sort works

We have an unsorted array arr = [ 1, 4, 2, 5, -2, 3 ] the task is to sort the array using bubble sort. 

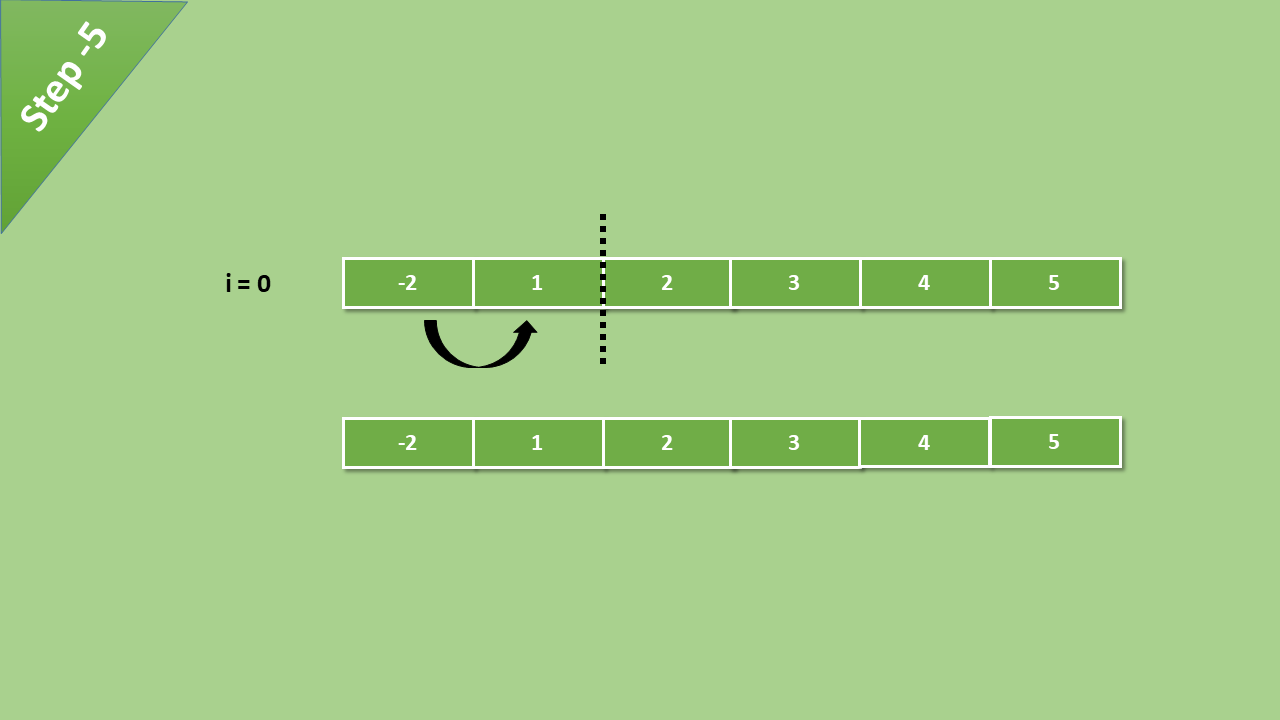
Bubble sort compares the element from index 0 and if the 0th index is greater than 1st index then the values get swapped and if the 0th index is less than the 1st index then nothing happens.

then, the 1st index compares to the 2nd index then the 2nd index compares to the 3rd, and so on…

let’s see it with an example, each step is briefly illustrated here

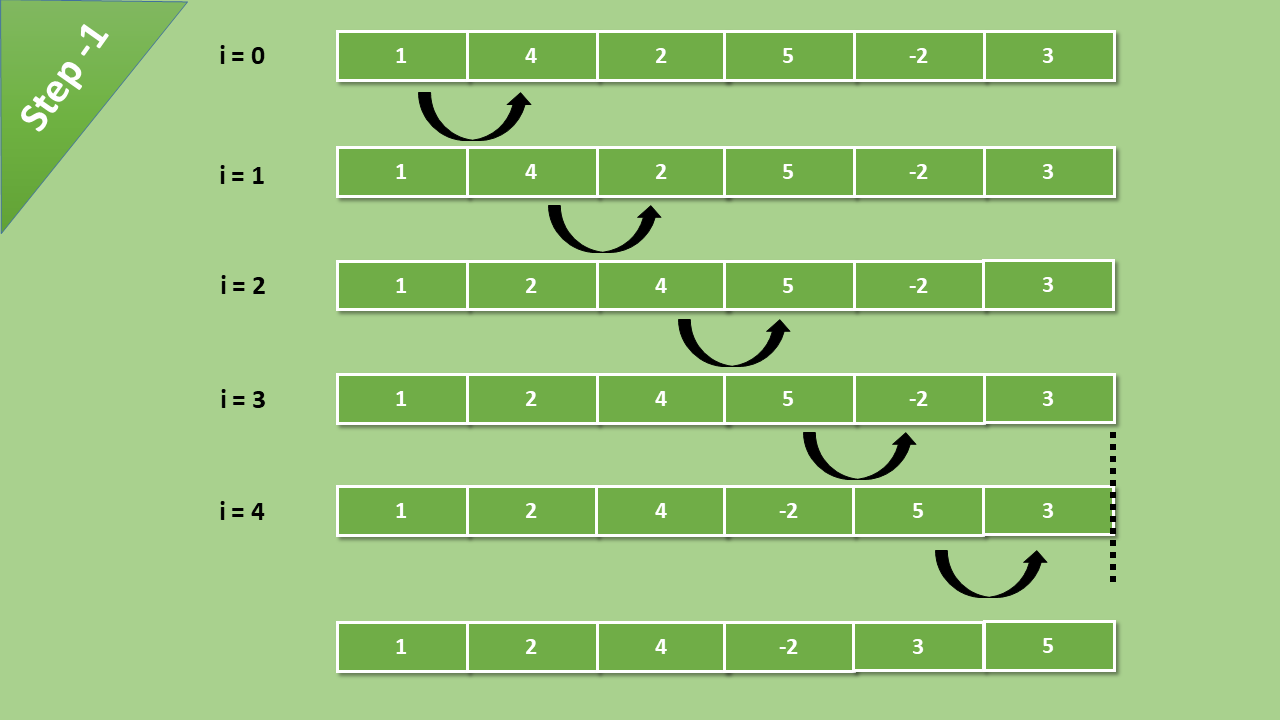
Comparisons happen till the last element of the array

After each iteration, the greatest value of the array becomes the last index of the array. in each iteration, the comparison happens till the last unsorted element.

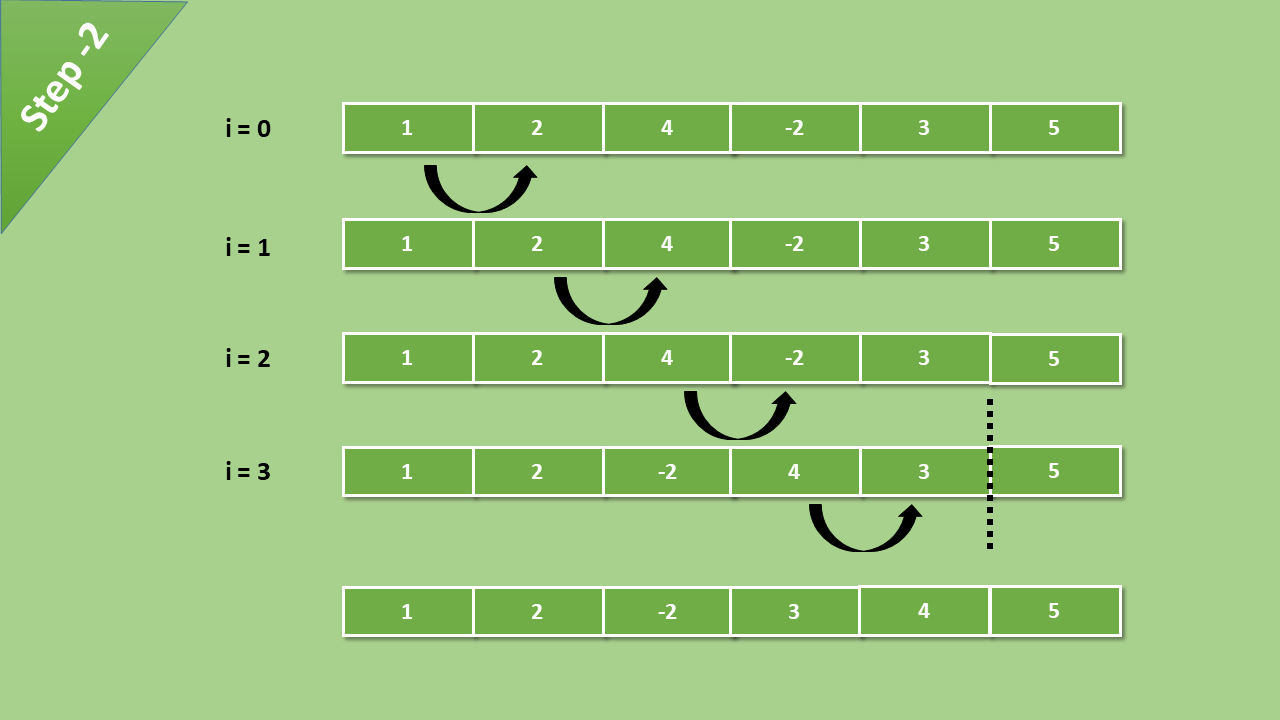
Now comparison reduced one step because the biggest element is at its right place

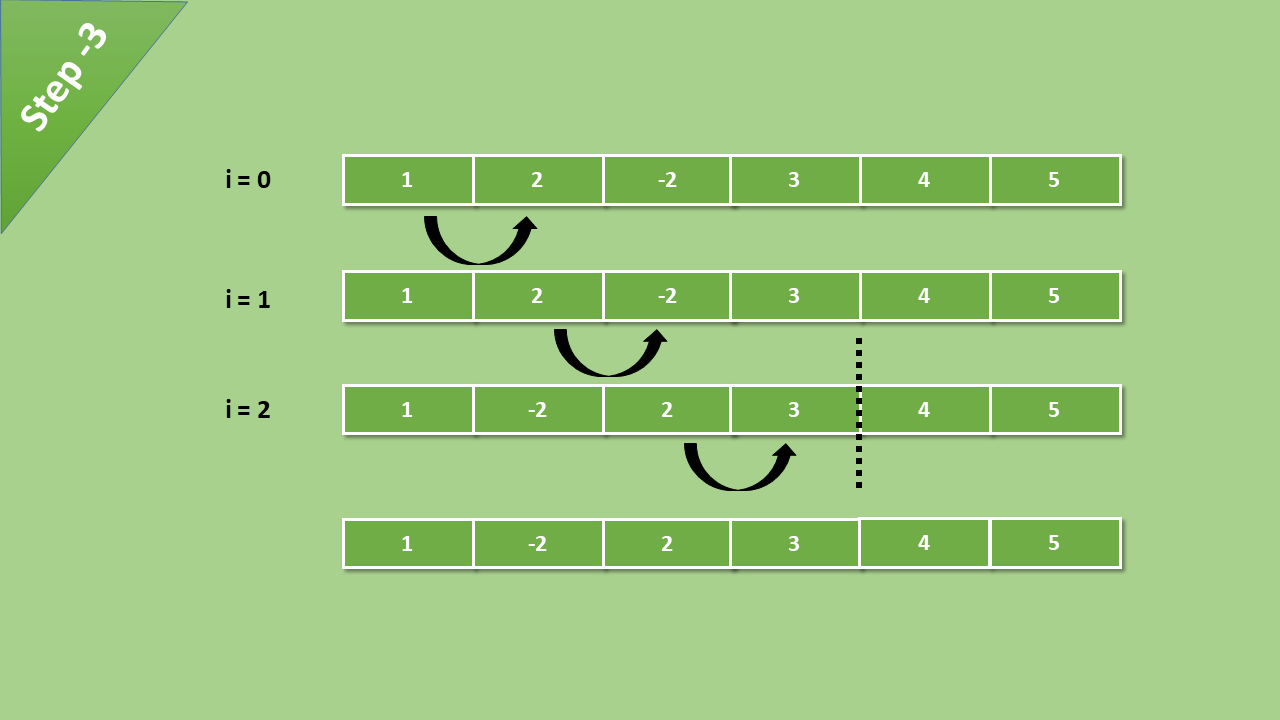
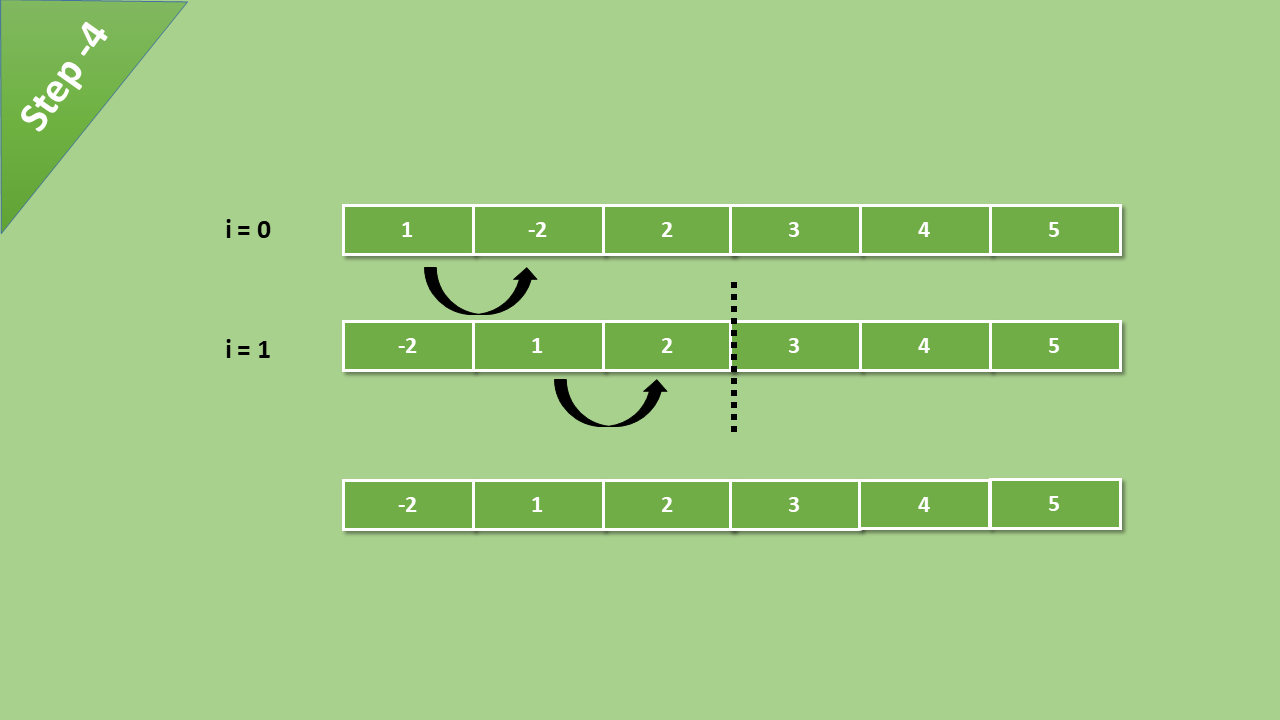
After all the iteration and comparisons of elements, we get a sorted array.

Syntax

BubbleSort(array){
  for i -> 0 to arrayLength 
     for j -> 0 to (arrayLength - i - 1)
      if arr[j] > arr[j + 1]
        swap(arr[j], arr[j + 1])
}

Implementation 

Javascript

// Bubble sort Implementation using Javascript


// Creating the bblSort function
 function bblSort(arr){

 for(var i = 0; i < arr.length; i++){

   // Last i elements are already in place
   for(var j = 0; j < ( arr.length - i -1 ); j++){

     // Checking if the item at present iteration
     // is greater than the next iteration
     if(arr[j] > arr[j+1]){

       // If the condition is true then swap them
       var temp = arr[j]
       arr[j] = arr[j + 1]
       arr[j+1] = temp
     }
   }
 }
 // Print the sorted array
 console.log(arr);
}


// This is our unsorted array
var arr = [234, 43, 55, 63,  5, 6, 235, 547];


// Now pass this array to the bblSort() function
bblSort(arr);

Output 
Sorted array :
[5, 6, 43, 55, 63, 234, 235, 547]

Note: This implementation is not optimized. We will see the optimized solution next.

Optimized Solution

As we discussed the implementation of bubble sort earlier that is not optimized. Even If the array is sorted, the code will run with O(n^2) complexity. Let’s see how to implement an optimized bubble sort algorithm in javascript.

The syntax for Optimized solution

BubbleSort(array){
  for i -> 0 to arrayLength 
     isSwapped <- false
     for j -> 0 to (arrayLength - i - 1)
      if arr[j] > arr[j + 1]
        swap(arr[j], arr[j + 1])
        isSwapped -> true
}

Implementation

Javascript

// Optimized implementation of bubble sort Algorithm

function bubbleSort(arr){

  var i, j;
  var len = arr.length;

  var isSwapped = false;

  for(i =0; i < len; i++){

    isSwapped = false;

    for(j = 0; j < len; j++){
        if(arr[j] > arr[j + 1]){
          var temp = arr[j]
          arr[j] = arr[j+1];
          arr[j+1] = temp;
          isSwapped = true;
        }
    }

    // IF no two elements were swapped by inner loop, then break

    if(!isSwapped){
      break;
    }
  }

  // Print the array
  console.log(arr)
}


var arr = [243, 45, 23, 356, 3, 5346, 35, 5];

// calling the bubbleSort Function
bubbleSort(arr)

Output
Sorted Array :
[3, 5, 23, 35, 45, 243, 356, 5346]

Complexities

Worst Case and Average case time complexity 

If the array is in reverse order then this condition is the worst case and Its time complexity is O(n²).

Best case time complexity

If the array is already sorted then it is the best-case scenario and its time complexity is O(n)

Auxiliary Space: O(1)