Our atmosphere extends to many kilometers above water level. The weight of the air acts as pressure referred to as air pressure. The pressure in our body balances the air pressure which is why we don’t feel it. Around the earth’s surface, a layer of gases is there. The air present in the atmosphere exerts pressure on the earth which is called atmospheric pressure. 1.01325 Pascal is the value of atmospheric pressure at sea level. The air pressure keeps on increasing as we move towards the Earth’s surface. Due to the large surface area of the atmosphere around the earth, the amount of atmospheric pressure upon us is quite large, but we do not feel any of its effects. This is so because the pressure of the air inside our body is adequate to the air pressure. There are also fluids present in our body that exert pressure inside our body. Hence, our bodies easily obtain a balance with air pressure. However, sometimes nose bleeding occurs at higher altitudes where the atmospheric pressure is low as compared to that at the Earth’s surface (low altitudes). This is so because at that point the vital sign in our body becomes above the air pressure outside us.
Atmosphere- The gaseous envelope surrounding the earth from all around is called the atmosphere. It extends approximately up to 400 km. It contains air which is 72% nitrogen and 21% oxygen additionally to a little proportion of dioxide, chemical element, etc.
Atmospheric pressure- Air possesses weight and hence it exerts pressure like liquids because it possesses weight. The atmospheric pressure at a point is defined as the force acting normally on a unit area around that point, due to the total height of the air column of the atmosphere above it.
The value of it is maximum at sea level and decreases as we go to higher altitudes.
Its symbol is Pa and S.I. unit is newton per square meter (N m-2) or pascal (Pa).
Pa = 1.013 × 105 Nm-2.
Surface Pressure
The surface pressure is defined as the difference in interfacial tension between a clean interface and an interface in the presence of an emulsifier. The air pressure at a location on the surface (terrain and oceans) is called surface pressure, and it is proportional to the mass of air over that location.
Atmospheric models like general circulation models (GCMs) usually predict the non-dimensional logarithm of surface pressure, for numerical reasons.
On Earth, the average value of surface pressure is 985 hPa. The average pressure at mean sea level (MSL) within the International atmosphere (ISA) is 1013.25 hPa, or 1 atmosphere (atm), or 29.92 inches of mercury.
Pressure (p), mass (m), and the acceleration due to gravity (g), where A is the surface area are related by P = 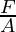 =
=  . Atmospheric pressure is thus proportional to the load per unit area of the atmospheric mass above that location.
. Atmospheric pressure is thus proportional to the load per unit area of the atmospheric mass above that location.

Sea Level Pressure
The air pressure is adequate to the pressure exerted by a mercury column of height “h”. Atmospheric pressure = h × d × g, where h is the height of the mercury column, d the density of mercury, and g the acceleration due to gravity.
Atmospheric Pressure =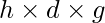 = 0.76 × 13600 × 9.8 = 101293 Pa.
= 0.76 × 13600 × 9.8 = 101293 Pa.
Standard sea-level pressure equals to 760 mm of mercury or 29.92 inches, 14.70 pounds per square inch, 1,013.25 × 103 dynes per square centimeter, 1,013.25 millibars, one standard atmosphere, or 101.325 kilopascals.
Mean Sea Level Pressure
The mean sea-level pressure (MSLP) is that the air pressure at the mean water level (PMSL). Normally in weather reports on radio, television, and newspapers or the Internet we see this atmospheric pressure. When barometers within the home are set to match the local weather reports, they display pressure adjusted to water level, not the particular local air pressure.
The altimeter setting in aviation is an air pressure adjustment.
1013.25 mbar (101.325 kPa; 29.921 in Hg; 760.00 mmHg) average sea-level pressure. Weather reports (METAR), QNH is transmitted around the world in millibars or hectopascals (1 hectopascal = 1 millibar), except within the US, Canada, and Colombia where it’s reported in inches of mercury (to two decimal places), in aviation. The US and Canada also report sea-level pressure SLP, which is adjusted to water level by a special method, within the remarks section, not within the internationally transmitted part of the code, in hectopascals or millibars. However, in Canada’s public weather reports, water level pressure is instead reported in kilopascals.
In the US weather code remarks, three digits are all that are transmitted; decimal points and therefore the one or two most vital digits are omitted: 1013.2 mbar (101.32 kPa) is transmitted as 132; 1000.0 mbar (100.00 kPa) is transmitted as 000; 998.7 mbar is transmitted as 987; etc. the very best sea-level pressure on Earth occurs in Siberia, with record highs on the brink of 1085 mbar (108.5 kPa; 32.0 in Hg), where the Siberian High often attains a sea-level pressure above 1050 mbar (105 kPa; 31 in Hg). rock bottom measurable sea-level pressure is found at the centers of tropical cyclones and tornadoes, with a record low of 870 mbar (87 kPa; 26 in Hg).
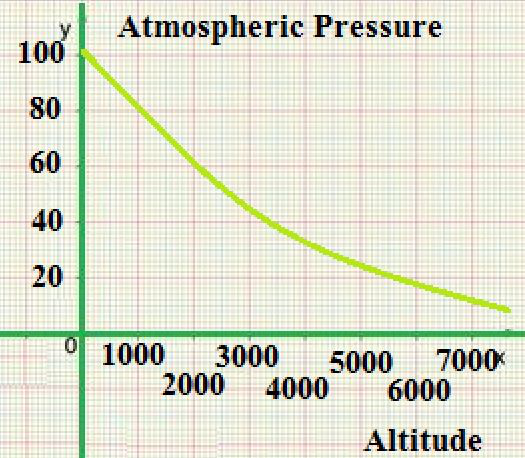
Variation in Altitude
Pressure on Earth varies with the altitude of the surface, so air pressure on mountains is usually lower than the air pressure on ground level. Pressure varies smoothly from the surface to the very best of the mesosphere. Although the pressure changes with the weather, NASA has averaged the conditions for all parts of the world year-round. As altitude increases, air pressure decreases. At a given altitude one can calculate the atmospheric pressure. Temperature and humidity also affect the air pressure, and it’s necessary to understand these to compute an accurate figure. The graph at right was developed for a temperature of 15 °C and a humidity of 0%.
The pressure decreases by about 1.2 kPa (12 hPa) for every 100 meters, at low altitudes above water level. For higher altitudes within the troposphere, the next equation (the barometric formula) relates atmospheric pressure p to altitude h:
p = 
=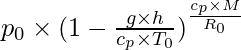

Barometer
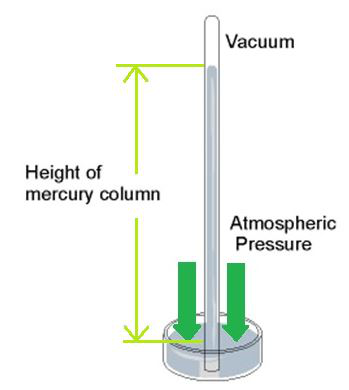
The earth’s air pressure at an associate degree given place is measured with an instrument known as the measuring instrument. The barometer is a perfect and commonplace instrument to measure air pressure. Within the barometer, the modification within the pressure is indicated on a dial by a pointer. The barometer was fictitious by physicists around 1644.
A simple measuring instrument consists of a glass tube of length 100 cm with one finish closed, and a trough with mercury. The tube is stuffed with pure and dry mercury. Its open finish is closed with a thumb and inverted vertically within the trough stuffed with mercury.
It is ascertained that a number of the mercury from the glass tube flows down into the trough and a set length of mercury column remains within the tube. The empty area on top of the mercury column is named the Torricellian vacuum.
Consider 2 points, “A” and “B” on the surface of the mercury. Note that each point square measures at an identical level. There’s the air on top of purpose “A” and also the mercury column on top of purpose “B”. PA is that the pressure exerted by the atmosphere at purpose A and the metallic element is that the pressure exerted by the peak of the mercury column within the tube at purpose B. Since “A” and “B” square measure on an identical horizontal plane,
PA = PB.
Therefore, the air pressure is expressed in terms of the length of the mercury column. The air pressure level is 76 cm of mercury. The standard air pressure on the surface varies between 940 and 1040 hPa (mbar). The standard air pressure at ground level is 1013 hPa (mbar).
Applications
Barometric pressure and thus the pressure tendency (the change of pressure over time) are utilized in meteorology since the late 19th century. When utilized together with wind observations, reasonably accurate short-term forecasts are often made. Simultaneous barometric readings from across a network of weather stations allow maps of air pressure to be produced, which were the first kind of fashionable weather maps when created within the 19th century. Isobars, lines of equal pressure, when drawn on such a map, provide a relief map showing areas of high and low. Low-level wind convergence into the surface brings clouds and sometimes precipitation causes atmospheric lift. The larger the change in pressure, especially if quite 3.5 hPa (0.1 inHg), the greater the change in weather which can be expected. If the pressure drop is rapid, a low-pressure system is approaching, and there’s a greater chance of rain. Rapid pressure rises, like within the wake of a chilly front, are related to improving weather, like clearing skies.
With falling atmospheric pressure, gases trapped within the coal in deep mines can escape more freely. Thus low increases the danger of firedamp accumulating. Collieries, therefore, keep track of the pressure.
Android barometers are utilized in skin diving. A submersible pressure gauge is employed to stay track of the contents of the diver’s air tank. Another gauge is used to measure the hydrostatic pressure, usually expressed as a depth of seawater. Either or both gauges could even be replaced with electronic variants or a dive computer.
Equation of Air Pressure
When air pressure is measured by a barometer, the pressure is additionally mentioned because of the “barometric pressure”. Assume a barometer with a cross-sectional area A, a height h, full of mercury from the lowest at Point B to the very best at Point C. The pressure at the rock bottom of the barometer, Point B, is capable of the air pressure. The pressure at the very top, Point C, is often taken as zero because there’s only mercury vapor above now and its pressure is extremely low relative to the atmospheric pressure. Therefore, one can find the air pressure using the barometer and this equation:
Patm = ρgh
Where the density of mercury is ρ, the gravitational acceleration is g, and the height of the mercury column above the free surface area is h. The physical dimensions (length of the tube and cross-sectional area of the tube) of the barometer itself do not affect the height of the fluid column in the tube.
In thermodynamic calculations, a commonly used unit of measurement is the “standard atmosphere”. At 0 °C this is the pressure resulting from a column of mercury of 760 mm in height. Use ρHg = 13,595 kg/m3 for the density of mercury and use g = 9.807 m/s2 for gravitational acceleration.
If water were used (instead of mercury) to satisfy the quality air pressure, a water column of roughly 10.3 m (33.8 ft) would be needed.
Standard atmospheric pressure as a function of elevation:
Note: 1 torr = 133.3 Pa = 0.03937 in Hg
Sample Questions
Question 1. At a given place, a mercury barometer records a pressure of 0.50 m of Hg. If mercury in the barometer is replaced by water What would be the height of the water column? Take R.D. of mercury = 13.6.
Solution:
Relative Density of Hg = 1.36 = 13.6 × 103 kg/m3
Acceleration due to gravity, g = 9.8 m/s2
Height of mercury column = 0.50 m
Pressure, P = ρgh
Or, P = {0.5×(1.36×103)×9.8} pascal
Or, P = 6.664 × 103
Let h be the height of the water column
Then, P = h x density of water x g
Or, 6.664 × 103 = h × 103 × 9.8
Or, h = 0.68 m
Question 2. The atmospheric pressure is 76 cm of Hg at sea level. What is the height of a hill where the barometer reads 60 cm Hg if air pressure falls by 10 mm of Hg per 120m of ascent? State the assumption made by you.
Solution:
Atmospheric pressure, P = 76 cm Hg
Pressure falling rate = 10 mm of hg per 120 m of ascent = 1 cm of Hg per 120 m of ascent
The pressure at hill, P` = 60 cm Hg
Total fall in pressure = P – P` = (76-60) cm Hg = 16 cm Hg
Now, the fall in pressure is 1 cm Hg for every 120 m increases in height.
Thus, if the fall in pressure is 6 cm Hg increase in height shall be (16 × 120) m = 1920 m
Question 3. The atmospheric pressure is 1.04 × 105 Pa at sea level. Assuming the density of air to be unvarying and alike to 1.6 kg m-3 and g = 10 m s-2, find the height of the atmosphere.
Solution:
Atmospheric pressure, P = 1.04 × 105 Pa
g = 10 m s-2
Density, ρ = 1.6 kg m-3
Let h be the height of the atmosphere.
P = ρgh
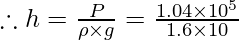 = 6500 m
= 6500 m
Question 4. At a height of 108 m above the sea level assuming the density of air to be 1.36 kg m-3 find the fall in barometric height in mm of Hg. Take density of Hg = 13.6 × 103 kg m-3.
Solution:
Let h = 108 m be the height above sea level
Ph – Psea = ρair gh
Or, ρmghf – ρmghi = ρairgh
Or, ρmg × Δh = ρairgh
Or,  = 10.8 x 10-6 mm of Hg
= 10.8 x 10-6 mm of Hg
Question 5. Convert 2 mm of Hg into pascal. Take the density of Mercury, Hg = 13.6 × 103 kg m-3 and gravitation, g = 9.8 m s-2.
Solution:
Density of Mercury, Hg = 13.6 × 103 kg m-3
Acceleration due gravity, g = 9.8 m s-2
Height of the mercury column = 2mm = 0.002 m
Therefore, Pressure, P = hρg
or, P = 0.002 × (13.6 × 103) × 9.8 pascal
or, P = 254.8 Pa
Question 6. Solve the following:
(a) Calculate the height of a column of water which will exert on its base the same pressure as the 72.5cm column of Hg. The density of Hg is 13.6g cm-3.
(b) If the cross-section of the water column is made wider will the height of the water column in the previous part change?
Solution:
(a) We know that the pressure exerted by the water column, P = hρg
The density of water = 1
As the pressure of H2O and Hg is the same,
hw ρw g = hm ρm g
hw × 1 × g = hm ρm g
hw = hm ρm
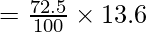
= 9.86
Height of the water column = 9.86m
(b) The height of the water column will be unaffected if the water column is made wider.
Question 7. The water pressure on the bottom floor is 60,800 Pa and on the primary floor is 15,800 Pa. Find the height of the first floor. (Take: density of H2O = 1000kg m-3, g = 10m/s2)
Solution:
To find the height of the first floor:
Given: Pw on ground floor Pwg = 60,800 Pa
Pw on first-floor Pwf = 15,800Pa
From the formula of pressure:
P = hρg
In order to know the height of the first floor, we have to calculate the difference in pressure
P = Pwg – Pwf
= 60800 – 15800
= 45000Pa
Substituting this value in the formula for the pressure to calculate height:
P = hρg
45000 = 1000 × 10 × h
h = 4.5m
The height of the floor is 4.5m.
Share your thoughts in the comments
Please Login to comment...