Abstract Data Types
Last Updated :
23 Sep, 2023
In this article, we will learn about ADT but before understanding what ADT is let us consider different in-built data types that are provided to us. Data types such as int, float, double, long, etc. are considered to be in-built data types and we can perform basic operations with them such as addition, subtraction, division, multiplication, etc. Now there might be a situation when we need operations for our user-defined data type which have to be defined. These operations can be defined only as and when we require them. So, in order to simplify the process of solving problems, we can create data structures along with their operations, and such data structures that are not in-built are known as Abstract Data Type (ADT).
Abstract Data type (ADT) is a type (or class) for objects whose behavior is defined by a set of values and a set of operations. The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented. It does not specify how data will be organized in memory and what algorithms will be used for implementing the operations. It is called “abstract” because it gives an implementation-independent view.
The process of providing only the essentials and hiding the details is known as abstraction.
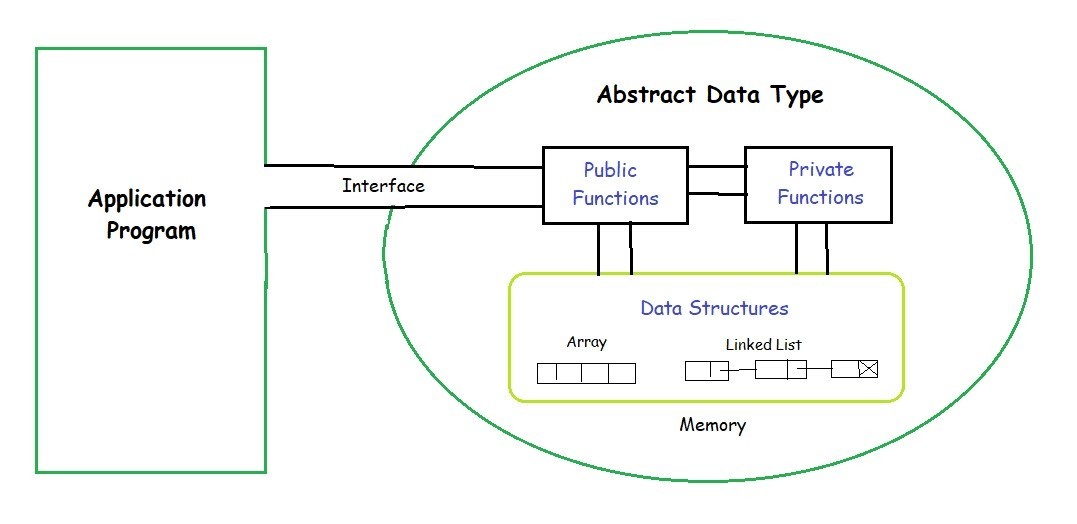
The user of data type does not need to know how that data type is implemented, for example, we have been using Primitive values like int, float, char data types only with the knowledge that these data type can operate and be performed on without any idea of how they are implemented.
So a user only needs to know what a data type can do, but not how it will be implemented. Think of ADT as a black box which hides the inner structure and design of the data type. Now we’ll define three ADTs namely List ADT, Stack ADT, Queue ADT.
1. List ADT

Vies of list
- The data is generally stored in key sequence in a list which has a head structure consisting of count, pointers and address of compare function needed to compare the data in the list.
- The data node contains the pointer to a data structure and a self-referential pointer which points to the next node in the list.
- The List ADT Functions is given below:
- get() – Return an element from the list at any given position.
- insert() – Insert an element at any position of the list.
- remove() – Remove the first occurrence of any element from a non-empty list.
- removeAt() – Remove the element at a specified location from a non-empty list.
- replace() – Replace an element at any position by another element.
- size() – Return the number of elements in the list.
- isEmpty() – Return true if the list is empty, otherwise return false.
- isFull() – Return true if the list is full, otherwise return false.
2. Stack ADT

View of stack
- In Stack ADT Implementation instead of data being stored in each node, the pointer to data is stored.
- The program allocates memory for the data and address is passed to the stack ADT.
- The head node and the data nodes are encapsulated in the ADT. The calling function can only see the pointer to the stack.
- The stack head structure also contains a pointer to top and count of number of entries currently in stack.
- push() – Insert an element at one end of the stack called top.
- pop() – Remove and return the element at the top of the stack, if it is not empty.
- peek() – Return the element at the top of the stack without removing it, if the stack is not empty.
- size() – Return the number of elements in the stack.
- isEmpty() – Return true if the stack is empty, otherwise return false.
- isFull() – Return true if the stack is full, otherwise return false.
3. Queue ADT

View of Queue
- The queue abstract data type (ADT) follows the basic design of the stack abstract data type.
- Each node contains a void pointer to the data and the link pointer to the next element in the queue. The program’s responsibility is to allocate memory for storing the data.
- enqueue() – Insert an element at the end of the queue.
- dequeue() – Remove and return the first element of the queue, if the queue is not empty.
- peek() – Return the element of the queue without removing it, if the queue is not empty.
- size() – Return the number of elements in the queue.
- isEmpty() – Return true if the queue is empty, otherwise return false.
- isFull() – Return true if the queue is full, otherwise return false.
Features of ADT:
Abstract data types (ADTs) are a way of encapsulating data and operations on that data into a single unit. Some of the key features of ADTs include:
- Abstraction: The user does not need to know the implementation of the data structure only essentials are provided.
- Better Conceptualization: ADT gives us a better conceptualization of the real world.
- Robust: The program is robust and has the ability to catch errors.
- Encapsulation: ADTs hide the internal details of the data and provide a public interface for users to interact with the data. This allows for easier maintenance and modification of the data structure.
- Data Abstraction: ADTs provide a level of abstraction from the implementation details of the data. Users only need to know the operations that can be performed on the data, not how those operations are implemented.
- Data Structure Independence: ADTs can be implemented using different data structures, such as arrays or linked lists, without affecting the functionality of the ADT.
- Information Hiding: ADTs can protect the integrity of the data by allowing access only to authorized users and operations. This helps prevent errors and misuse of the data.
- Modularity: ADTs can be combined with other ADTs to form larger, more complex data structures. This allows for greater flexibility and modularity in programming.
Overall, ADTs provide a powerful tool for organizing and manipulating data in a structured and efficient manner.
Abstract data types (ADTs) have several advantages and disadvantages that should be considered when deciding to use them in software development. Here are some of the main advantages and disadvantages of using ADTs:
Advantages:
- Encapsulation: ADTs provide a way to encapsulate data and operations into a single unit, making it easier to manage and modify the data structure.
- Abstraction: ADTs allow users to work with data structures without having to know the implementation details, which can simplify programming and reduce errors.
- Data Structure Independence: ADTs can be implemented using different data structures, which can make it easier to adapt to changing needs and requirements.
- Information Hiding: ADTs can protect the integrity of data by controlling access and preventing unauthorized modifications.
- Modularity: ADTs can be combined with other ADTs to form more complex data structures, which can increase flexibility and modularity in programming.
Disadvantages:
- Overhead: Implementing ADTs can add overhead in terms of memory and processing, which can affect performance.
- Complexity: ADTs can be complex to implement, especially for large and complex data structures.
- Learning Curve: Using ADTs requires knowledge of their implementation and usage, which can take time and effort to learn.
- Limited Flexibility: Some ADTs may be limited in their functionality or may not be suitable for all types of data structures.
- Cost: Implementing ADTs may require additional resources and investment, which can increase the cost of development.
Overall, the advantages of ADTs often outweigh the disadvantages, and they are widely used in software development to manage and manipulate data in a structured and efficient way. However, it is important to consider the specific needs and requirements of a project when deciding whether to use ADTs.
From these definitions, we can clearly see that the definitions do not specify how these ADTs will be represented and how the operations will be carried out. There can be different ways to implement an ADT, for example, the List ADT can be implemented using arrays, or singly linked list or doubly linked list. Similarly, stack ADT and Queue ADT can be implemented using arrays or linked lists.
Share your thoughts in the comments
Please Login to comment...