Cuboid is a three-dimensional solid object. It is also referred as a regular hexahedron and is one of the five platonic solids. All the edges share at least a common edge with each other. The structure of a cuboid can be defined in terms of the fact that each of the faces is being connected to four vertices and four edges, vertex connected with three edges and three faces, and edges are in touch with two faces and two vertices. The length, breadth, or height may or may not be equal in the case of a cuboid.
Properties of Cuboid
- All the faces are rectangular in nature.
- All the angles are at right angles
- Opposite faces of a cuboid are equal.
Volume of Cuboid
The volume of a cuboid is equivalent to the amount of space occupied within the figure. The volume of any three-dimensional figure is dependent on the three edges’ length, that is, its length, breadth, and height. It can be considered to be a solid rectangle. Let us assume the height of the cuboid to be h, l its length and breadth to be denoted by b units respectively.
In addition to this, let us assume V to be the volume of the cuboid. Deriving its formula,
The volume of cuboid = Base area × Height
The base area for cuboid = l × b
Hence,
Volume of a cuboid, V = Product of all three sides = l × b × h = lbh

Surface area of Cuboid
A cuboid is denoted by the following two kinds of surface areas:
- Total Surface Area – The summation of the area of each face. Denoted by S.
Total Surface Area of Cuboid, S = 2 × (lb + bh + lh)
- Lateral Surface Area – The summation of the area of each face excluding the base and the top. Denoted by L.
The total surface area and lateral surface area can be expressed in terms of length (l), breadth(b), and height of cuboid(h) as:
Lateral Surface Area of Cuboid, L = 2h (l + b)
What would happen to the volume and surface area of a cuboid if all its dimensions are doubled?
Solution:
Let us assume l, b, h to be the length, breadth, height of the first cuboid respectively.
Let us assume L, B, H to be the length, breadth, height of the new cuboid formed.
Since all the sides of the cuboid are doubled, therefore, we have,
We know that,
L = 2l
B = 2b
H = 2h
Computation of surface area
Surface area of the first cuboid S = 2(lb + bh + hl)
Now,
Surface area of new cuboid S,
= 2(LB + BH + HI)
= 2[(2l)(2b) + (2b)(2h) + (2h)(2l)]
= 2(4lb + 4bh + 4hl)
= 4[2(lb + bh + hl)]
= 4S
∴ The surface area of the new cuboid is 4S.
Computation of volume
Volume of the original cuboid is given by V = l × b × h
When its length is doubled, its length becomes 2 × l.
When its height is double, it becomes 2 × h.
When its breadth is double, it becomes 2 × b.
Now, Volume of the new cuboid = length × breadth × height
= 2 × l × 2 × b × 2 × h
= 8 × l × b × h
∴ Therefore, the volume of the new cuboid is eight times the initial volume.
Sample Questions
Question 1. Calculate the volume of cuboid if its Length is doubled, Height is doubled and Breadth is the same?
Solution:
Assume that,
Length of cuboid = l
Height of cuboid = h
Breadth of cuboid = b
Therefore,
Volume of cuboid = Length × Breadth × Height
= l × b × h
According to the question
Length of cuboid is doubled = 2 × l = 2l
Height of cuboid is doubled = 2 × h = 2h
Breadth remains same
Further,
Volume of the cuboid with the new dimensions = Length × Breadth × Height
= 2 × l × b × 2 × h
= 4 × l × b × h
Hence,
We can see that the volume of the cuboid with the new cuboid is four times the volume of the initial cuboid.
Question 2. Find out the volume of cuboid if its Length is doubled, height is the same and breadth is halved?
Solution:
Assume
Length of a cuboid = l
Breadth of a cuboid = b
Height of a cuboid = h
Therefore,
Volume of a cuboid = Length × Breadth × Height
= l × b × h
Further,
Length of cuboid is doubled = 2 × l = 2l
Breadth of cuboid is halved = 
Height of cuboid is same = h
Therefore,
Volume of new dimension cuboid = Length × Breadth × Height
= 2 × l ×  × h
× h
= l × b × h
Hence,
We can clearly see that after Length is doubled, height is the same and breadth is halved the volume of the cuboid remains the same.
Question 3. Consider that the surface area of a cuboid shoebox is 126 cm2. It is given that the length of the cuboid is 6 cm and the height of the cuboid is 3 cm, Then find the breadth of the cuboid shoe box.
Solution:
Here we are given that,
Surface area of the cuboid shoe box = 126 cm2
Length of the cuboid shoe box = 6 cm
Height of the cuboid shoe box = 3 cm
Assume Breadth of the cuboid shoe box = b cm
Thus,
⇒ 126 cm2 = 2 × {(Length × Breadth) + (Breadth × Height) + (Length × Height)}
⇒ 126 cm2 = 2 × {(6 × b) + (b × 3) + (6 × 3)}
⇒ 126 cm2 = 2 × (6b + 3b + 6 x 3)
⇒ 126 cm2 = 2 × (9b + 18)
⇒ 126 cm2 = 18b + 36
⇒ 18b = 126 – 36
⇒ 18b = 90
⇒ b = 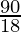
⇒ b = 5 cm
Therefore.
Breadth of the cuboid show box is 5 cm.
Question 4. What will happen to the surface area of a cuboid if its length, breadth, and height of a cuboid are tripled?
Solution:
Assume
Length of cuboid = l
Breadth of cuboid = b
Height of cuboid = h
Surface Area of Cuboid = 2 × {(Length × Breadth) + (Breadth × Height) + (Length × Height)}
According to the question
Length of cuboid tripled = 3 × length = 3l
Breadth of cuboid tripled = 3 × breadth = 3b
Height of cuboid tripled = 3 × height = 3h
Surface Area of a increased dimensional Cuboid = 2 × (3l × 3b + 3b × 3h +3l × 3h)
= 9 × 2 × (lb + bh + lh)
= 9 × Surface area of initial cuboid
Therefore,
We can see that if we triple all the dimensions of the cuboid then its surface area becomes 9 times.
Question 5. If the volume of a cuboid is 24 cm3. If all the dimensions are doubled then find the volume of the cuboid?
Solution:
Here we are given that,
Volume of cuboid = 24 cm3
According to the question
If we double all the dimensions of the cuboid
Then,
Volume of the cuboid = 24 × 2 × 2 × 2
= 192 cm2
Share your thoughts in the comments
Please Login to comment...