What will happen to the volume of a cube if its length is doubled?
Last Updated :
20 Nov, 2021
Cube is a three-dimensional shape that is associated with a certain occupied volume. It has six square faces, each of which corresponds to an equal length. It can be considered to be square sheets stacked together. Also known as a regular hexahedron, it is one of the five platonic solid shapes.
Volume of cube
The volume of a cube is a three-dimensional shape that occupies a certain volume of mass or space. The unit of volume of the cube is given as the (unit)3 or cubic units. The SI unit of volume is the cubic meter (m3).
Volume of Cube Using Edge Length
The measure of all the sides of a cube is the same thus, we only need to know one side in order to calculate the volume of the cube. The steps to calculate the volume of a cube using the side length are,
- Step 1: Take a noting of the edge length of the cube, say side.
- Step 2: Now, Volume of cube = (side)3.
- Step 3: The final answer is measured along with the cubic units.
Volume of Cube Formula
Volume of the cube = Side × Side × Side = Side3
What will happen to the volume of a cube if its length is doubled?
Solution:
Volume of the cube = Side3
Since,
All the sides of the cube are equal
Then if the length of a side of the cube is increased
So, the side of the cube becomes
Side of the cube = 2 × Side
Assume
Side of the cube be ‘s’
Side of the cube = 2s
Now,
Volume of the cube = 2s × 2s × 2s
Volume of the cube = (2s)3
Volume of the cube = 8s3
To find how many times the volume of the cube is increased
⇒ 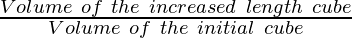
⇒ 8s3/ s3
⇒ 8
Therefore,
If the length of the cube is doubled then its volume is increased by 8 times.
Sample Questions
Question 1. What will happen if the side of the cube is decreased to half?
Solution:
As we know that
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Assume the side of the cube be ‘s’
Volume of the cube = s3
According to the question
The side of the cube is decreased to half
Therefore,
Side of the cube = s/2
Now,
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Volume of the decreased side cube = s/2 × s/2 × s/2
Volume of the decreased side cube = (s/2)3
Volume of the decreased side cube = s3/8
Therefore,
If we decrease the side of the cube to half then its volume is decreased by 8 times.
Question 2. If the side of the cube is tripled how many times the volume of the cube will be increased?
Solution:
As we know that
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Assume the side of the cube be ‘s’
Volume of the cube = s3
According to the question
The side of the cube is increased by 3 times
Therefore,
Side of the cube = 3 × s
Now,
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Volume of the decreased side cube = 3s × 3s × 3s
Volume of the decreased side cube = (3s)3
Volume of the decreased side cube = 27s3
Therefore,
If we increase the side of the cube to 3 times then its volume is increased by 27 times.
Question 3. Calculate the decrease in the volume of the cube if its side is decreased to 1/4?
Solution:
As we know that
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Assume the side of the cube be ‘s’
Volume of the cube = s3
According to the question
The side of the cube is decreased to 1/4
Therefore,
Side of the cube = s/4
Now,
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Volume of the decreased side cube = s/4 × s/4 × s/4
Volume of the decreased side cube = (s/4)3
Volume of the decreased side cube = s3/64
Therefore,
If we decrease the side of the cube by 1/4 then its volume decreases by 64 times.
Question 4. Find how many small cubes of side 2 cm can be made from a big cube of side 8 cm?
Solution:
As we know that
Volume of the cube = Side × Side × Side
Volume of the cube = Side3
Volume of small cube = 2 × 2 × 2
Volume of small cube = 8 cm3
Volume of big cube = 8 × 8 × 8
Volume of big cube = 512 cm3
To find how many small cubes can be made out of big cube
⇒ 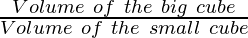
⇒ 512/8
⇒ 64
Therefore,
64 small cubes of side 2 cm can be made out of a big cube of side 8 cm.
Share your thoughts in the comments
Please Login to comment...