What is the expected number of flips to get two heads in a row?
Last Updated :
27 Oct, 2021
Probability is how likely an outcome occurs. The probability of an event is between 0 and 1 only and is also written in percentage. The probability of event A is often written as P(A).
Whenever we’re not sure about the outcome of an event, then we use probabilities of certain outcomes—how likely they occur. Analysis of these probabilities is called statistics. To understanding probability we take an example as flipping a coin:
There are two possible outcomes—heads or tails.
What’s the probability of the coin landing on tails? You might intuitively know that the likelihood is half/half or 50%.
Formula of Probability
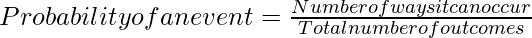
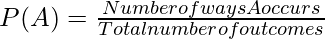
Types of Events
Equally Likely Events
The events having the same theoretical probability of occurring, then they are called equally likely events. The equally likely events have the same probability of occurring. For example, if we throw a die, then the probability of getting 2 is 1/6. Similarly, the probability of getting numbers from 1,2,3,4,5, and 6, one at a time is 1/6.
Complementary Events
Possibility of only two outcomes which states that an event will occur or not. Like a person will go or not go to the office, getting the bus or not getting the bus, etc. are examples of complementary events. Basically, the complement of an event occurring is the exact opposite to the probability of it is not occurring.
What is the expected number of flips to get two heads in a row?
Solution:
Probability of an event = (number of favorable event) / (total number of event).
P(B) = (Event B) / (total number of event).
Probability of getting a Head = 1/2.
Tossing a coin is an independent event, it is not dependent on how many times it’s been tossed.
Probability of getting 2 heads in a row = probability of getting head first time×probability of getting head second time.
Probability of getting 2 heads in a row = (1/2) × (1/2) = 1/4.
hence in 4 coins flip two heads in a row is possible.
Similar Questions
Question 1. How many times do you need to flip a coin to get two tails in a row?
Solution:
Probability of an event = (Number of ways it can occur) / (total number of outcomes),
P(B) = (Number of ways B can happen) / (Total number of outcomes),
Probability of getting a tails = 1/2.
Tossing a coin is an independent event, it is not dependent on how many times it’s been tossed.
Probability of getting 2 tails in a row = probability of getting tails first time×probability of getting tail second time.
Probability of getting 2 tails in a row = (1/2) × (1/2).
hence in 4 coins flip two tails in a row is possible.
Question 2. How many times do you need to flip a coin to get three tails in a row?
Solution:
Probability of an event = (Number of ways it can occur) / (total number of outcomes),
P(B) = (Number of ways B can happen) / (Total number of outcomes),
Probability of getting a tails = 1/2.
Tossing a coin is an independent event, it is not dependent on how many times it’s been tossed.
Probability of getting 3 tails in a row = probability of getting tail first time×probability of getting tail second time×probability of getting tail third time.
Probability of getting 3 tails in a row = (1/2) × (1/2) × (1/2).
Hence in 8 coin flip 3 tails in a row is possible.
Share your thoughts in the comments
Please Login to comment...