Two cubes have their volumes in the ratio 1:27, then find the ratio of their surface areas
Last Updated :
28 Nov, 2021
Cube is a three-dimensional figure composed of six square faces, facets, or sides, with three meeting at each vertex. There are square sheets stacked together that are characterized by three dimensions, being length, breadth, and height. All these dimensions are equivalent in length. There are 12 edges and 6 faces composing the cube.

Area of cube
The area of the cube is defined as the space enclosed within it. The area of any square sheet forming the faces of the cube is defined as the product of any two dimensions, such as length and breadth. Let us assume A to be the area of the cube. It is defined in terms of square units.
Now,
A = length × breadth
Since, all the sides of the cube are equal,
A = a × a
A = a2
Volume of cube
The volume of a cube is defined as the matter contained within the figure. It is the total quantity of the substance contained within the cube. The volume of a cube is defined as the product of all the dimensions of the cube, defined using its, length, breadth, and height. Volume of the cube is defined in terms of cubic units.
Now, since all the sides of the cube are equal,
Volume = length × breadth × height
Let us assume V to be the volume and a to be the same side of the cube.
V = a × a × a
V = a3
Two cubes have their volumes in the ratio 1:27, then find the ratio of their surface areas
Solution:
Let us assume a1 and a2 to be the side of cube1 and cube2 respectively.
Now,
Let the volume of cube1 be V1 and cube2 be V2 .
Upon equating,
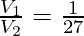
On solving,
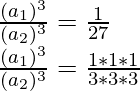
On taking the cube root, we get,
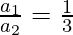
Let us assume the area A1 to be of cube1 and A2 of cube2.
On squaring both sides, we get,
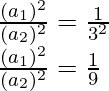
Therefore, the ratio of areas of both the cubes is 1 : 9.
Similar Questions
Question 1: Two cubes have volume in the ratio 1:64. The ratio of the sides of one cube to that of the other is?
Solution:
We have,
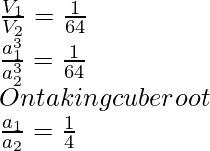
Therefore,
The ratio of their sides is 1:4.
Question 2: Find the ratio of areas according to the above problem.
Solution:
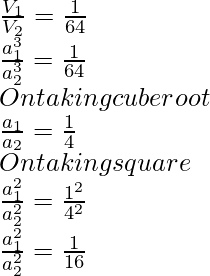
Therefore, the ratio of their areas is 1:16.
Question 3: Two cubes have volume in the ratio n:n/8. The ratio of the sides of one cube to that of the other is
Solution:
On simplifying the equation,
The volumes of the cubes are in the ratio 8n : n.
On striking off, n from both sides, we obtain the final ratio as 8:1.
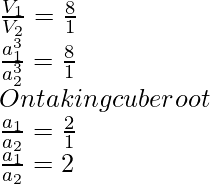
Question 4: Calculate the ratio of the area of a cube to its volume for a cube of side n.
Solution:
Area of a cube = n2
Volume of a cube = n3
The ratio of area : volume is equivalent to,
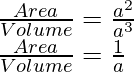
This implies that the volume is a times greater than area.
Question 5: If the volume of a cube with side 7 cm is 343 cm3. Calculate its area.
Solution:
Area is given by Volume/Side
= 343/7 cm2
= 49 cm2
Share your thoughts in the comments
Please Login to comment...