Transform string A into B by deleting characters from ends and reinserting at any position
Last Updated :
31 Mar, 2023
Given two strings A and B that are anagrams of each other, the task is to convert A to B if possible in minimum number of operations. An operation is defined as removing either the first or the last character in A and inserting it back anywhere in the string.
Examples:
Input: A = “edacb”, B = “abcde”
Output : 3
Explanation : The three operations are:
- We can remove “b” and insert it after “a” to get “edabc”
- We can remove “e” and insert it after “c” to get “dabce”
- We can remove “d” and insert it after “c” to get “abcde”
Input : A = “xyz”, B = “xyz”
Output : 0
Explanation : String A is equal to String B so no operation is required.
Approach: The approach is based on Dynamic Programming and Longest Common Subsequence (LCS)
Intuition:
- Instead of forming B from A by moving characters from the ends of A to the interior, we will attempt to form A from B by moving characters from B’s interior to its ends. It should be evident that the problem is equivalent.
- Now, after doing this reversed operation some number of times, we will have a resulting string B’ that we can split into three parts:
B’ = prefix + core + suffix
where- core consists of unmoved characters, and
- prefix / suffix are characters that have been moved to the beginning or end, respectively.
- Note that once we have moved a character, it is always suboptimal to move it again.
Since we are free to choose the order in which we move characters, we should choose to move the characters of prefix/suffix from the inside out.
Then, the cost of forming B’ from B in this way is len(prefix) + len(suffix). - The core is a subsequence of B : it consists of just the unmoved characters of B, in their original order. Indeed, this works both ways – we can turn any subsequence of B into a core, and arrange the remaining letters arbitrarily around it.
- Now our problem is to find a way to decompose A into those three parts:
- minimizing len(prefix) + len(suffix).
- maximize len(core) (the number of untouched characters).
- This can be restated as finding the maximum-length substring of A which is a subsequence of B.
Algorithm: This problem can be solved with Dynamic Programming much like the classic LCS (longest common subsequence) problem. See the comments in the code for the precise DP state. The main difference from LCS is that we cannot include dp[i-1][j] in dp[i][j], since that would break the contiguity of the A-substring.
Below is the implementation of the above approach :
C++
#include <bits/stdc++.h>
using namespace std;
int minOperations(string A, string B)
{
int dp[1001][1001];
int r = 0;
for (int i = 0; i <= A.size(); ++i) {
for (int j = 0; j <= B.size(); ++j) {
dp[i][j] = 0;
if (i && j) {
dp[i][j] = dp[i][j - 1];
if (A[i - 1] == B[j - 1]) {
dp[i][j] = max(
dp[i][j],
1 + dp[i - 1][j - 1]);
r = max(r, dp[i][j]);
}
}
}
}
return A.size() - r;
}
int main()
{
string A = "edacb";
string B = "abcde";
cout << minOperations(A, B);
return 0;
}
|
Java
import java.util.*;
public class GFG {
static int minOperations(String A, String B)
{
int[][] dp = new int[1001][1001];
int r = 0;
for (int i = 0; i <= A.length(); ++i) {
for (int j = 0; j <= B.length(); ++j) {
dp[i][j] = 0;
if (i > 0 && j > 0) {
dp[i][j] = dp[i][j - 1];
if (A.charAt(i - 1)
== B.charAt(j - 1)) {
dp[i][j] = Math.max(
dp[i][j], 1 + dp[i - 1][j - 1]);
r = Math.max(r, dp[i][j]);
}
}
}
}
return A.length() - r;
}
public static void main(String args[])
{
String A = "edacb";
String B = "abcde";
System.out.println(minOperations(A, B));
}
}
|
Python3
<script>
def minOperations(A, B) :
dp = [[ 0 for _ in range(1001)] for _ in range(1001) ]
r = 0
for i in range(0, len(A) + 1) :
for j in range(0, len(B) + 1) :
dp[i][j] = 0
if (i and j) :
dp[i][j] = dp[i][j - 1]
if (A[i - 1] == B[j - 1]) :
dp[i][j] = max(
dp[i][j],
1 + dp[i - 1][j - 1])
r = max(r, dp[i][j])
return len(A) - r
if __name__ == "__main__" :
A = "edacb"
B = "abcde"
print(minOperations(A, B))
|
C#
using System;
class GFG {
static int minOperations(string A, string B)
{
int[, ] dp = new int[1001, 1001];
int r = 0;
for (int i = 0; i <= A.Length; ++i) {
for (int j = 0; j <= B.Length; ++j) {
dp[i, j] = 0;
if (i > 0 && j > 0) {
dp[i, j] = dp[i, j - 1];
if (A[i - 1] == B[j - 1]) {
dp[i, j] = Math.Max(
dp[i, j], 1 + dp[i - 1, j - 1]);
r = Math.Max(r, dp[i, j]);
}
}
}
}
return A.Length - r;
}
public static void Main()
{
string A = "edacb";
string B = "abcde";
Console.Write(minOperations(A, B));
}
}
|
Javascript
<script>
function minOperations(A, B) {
let dp = new Array(1001);
for (let i = 0; i < dp.length; i++) {
dp[i] = new Array(1001)
}
let r = 0;
for (let i = 0; i <= A.length; ++i) {
for (let j = 0; j <= B.length; ++j) {
dp[i][j] = 0;
if (i && j) {
dp[i][j] = dp[i][j - 1];
if (A[i - 1] == B[j - 1]) {
dp[i][j] = Math.max(
dp[i][j],
1 + dp[i - 1][j - 1]);
r = Math.max(r, dp[i][j]);
}
}
}
}
return A.length - r;
}
let A = "edacb";
let B = "abcde";
document.write(minOperations(A, B));
</script>
|
Time Complexity : 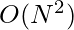
Auxiliary Space : 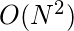
Efficient Approach : using array instead of 2d matrix to optimize space complexity
In previous code we can se that dp[i][j] is dependent upon dp[i-1][j-1] or dp[i][j-1] so we can assume that dp[i-1] is previous row and dp[i] is current row
Implementations Steps :
- Initialize an integer array dp of size 1001 with all elements as 0.
- Initialize a variable r to 0.
- Iterate over the characters of string A, and for each character, iterate over the characters of string B.
- For each (i, j) pair of indices, update dp[j] as follows:
a. If A[i] == B[j], then dp[j] = max(dp[j], prev + 1), where prev is the value of dp[j] before the update.
b. Otherwise, dp[j] = 0.
- After updating dp[j], update r as max(r, dp[j])
- The answer is A.size() – r, where A.size() is the length of string A.
- Return the answer.
Implementation :
C++
#include <bits/stdc++.h>
using namespace std;
int minOperations(string A, string B)
{
int dp[1001] = {0};
int r = 0;
for (int i = 0; i < A.size(); ++i) {
int prev = 0;
for (int j = 0; j < B.size(); ++j) {
int temp = dp[j];
dp[j] = max(dp[j], (A[i] == B[j]) ? prev + 1 : 0);
prev = temp;
r = max(r, dp[j]);
}
}
return A.size() - r;
}
int main()
{
string A = "edacb";
string B = "abcde";
cout << minOperations(A, B);
return 0;
}
|
Java
public class Main {
public static int minOperations(String A, String B) {
int[] dp = new int[1001];
int r = 0;
for (int i = 0; i < A.length(); ++i) {
int prev = 0;
for (int j = 0; j < B.length(); ++j) {
int temp = dp[j];
dp[j] = Math.max(dp[j], (A.charAt(i) == B.charAt(j)) ? prev + 1 : 0);
prev = temp;
r = Math.max(r, dp[j]);
}
}
return A.length() - r;
}
public static void main(String[] args) {
String A = "edacb";
String B = "abcde";
System.out.println(minOperations(A, B));
}
}
|
Python3
def minOperations(A, B):
dp = [0] * 1001
r = 0
for i in range(len(A)):
prev = 0
for j in range(len(B)):
temp = dp[j]
dp[j] = max(dp[j], prev + 1 if A[i] == B[j] else 0)
prev = temp
r = max(r, dp[j])
return len(A) - r
A = "edacb"
B = "abcde"
print(minOperations(A, B))
|
C#
using System;
class MainClass
{
public static int minOperations(string A, string B)
{
int[] dp = new int[1001];
int r = 0;
for (int i = 0; i < A.Length; ++i) {
int prev = 0;
for (int j = 0; j < B.Length; ++j) {
int temp = dp[j];
dp[j] = Math.Max(dp[j], (A[i] == B[j]) ? prev + 1 : 0);
prev = temp;
r = Math.Max(r, dp[j]);
}
}
return A.Length - r;
}
public static void Main(string[] args) {
string A = "edacb";
string B = "abcde";
Console.WriteLine(minOperations(A, B));
}
}
|
Javascript
function minOperations(A, B) {
let dp = new Array(1001).fill(0);
let r = 0;
for (let i = 0; i < A.length; ++i) {
let prev = 0;
for (let j = 0; j < B.length; ++j) {
let temp = dp[j];
dp[j] = Math.max(dp[j], A[i] == B[j] ? prev + 1 : 0);
prev = temp;
r = Math.max(r, dp[j]);
}
}
return A.length - r;
}
let A = "edacb";
let B = "abcde";
console.log(minOperations(A, B));
|
Time Complexity : O(N^2)
Auxiliary Space : O(N)
Share your thoughts in the comments
Please Login to comment...