RD Sharma Class 8 – Chapter 1 Rational Numbers – Exercise 1.1
Last Updated :
21 Feb, 2023
Question 1. Add the following rational numbers:
(i) -5 / 7 and 3 / 7
Solution:
(-5 / 7) + 3 / 7
Since denominators are the same hence numerators will be directly added considering their sign.
Therefore, (-5 + 3) / 7 = (-2) / 7
(ii) -15 / 4 and 7 / 4
Solution:
Denominators are same so numerators are directly added.
= (-15) / 4 + 7 / 4
= (-15 + 7) / 4
= (-8) / 4
= (4 * (-2)) / 4
= (-2)
(iii) -8 / 11 and -4 / 11
Solution:
As denominators are the same numerators are added along with their sign.
= (-8) / 11 + (-4) / 11
= (-8 – 4) / 11 (integers with same sign are added)
= (-12) / 11
(iv) 6 / 13 and -9 / 13
Solution:
As, denominators are same numerators are added with their sign.
= 6 / 13 + (-9) / 13
= (6 – 9) / 13 (integers with opposite sign)
= (-3) / 13
Question 2. Add the following rational numbers:
(i) 3 / 4 and -5 / 8
Solution:
Denominators are different, so we need to take the LCM of denominators to make them into like fractions.
LCM of 4 and 8 = 8
= 3 / 4 + (-5) / 8
= (3 × 2 + (-5)) / 8
= (6 – 5) / 8
= 1 / 8
(ii) 5 / -9 and 7 / 3
Solution:
Denominators are different, so we need to take the LCM of denominators to make them into like fractions.
LCM of 9 and 3 = 9
= (-5 / 9) + 7 / 3
= (-5 + 7 × 3) / 9
= (-5 + 21) / 9
= 16 / 9
(iii) -3 and 3 / 5
Solution:
Denominators are different, so we need to take the LCM of denominators to make them into like fractions.
= (-3) / 1 + 3 / 5
LCM of 1 and 5 = 5
= ((-3) × 5 + 3) / 5
= (-15 + 3) / 5
= (-12) / 5
(iv) -7 / 27 and 11 / 18
Solution:
LCM of 27 and 18
27 = 3 × 3 × 3
18 = 2 × 3 × 3
LCM = 3 × 3 × 3 × 2 = 54
Therefore,
= (-7) / 27 + 11 / 18
= ((-7 × 2 + 11 × 3)) / 54
= (-14 + 33) / 54
= 19 / 54
(v) 31 / -4 and -5 / 8
Solution:
LCM of 4 and 8 = 8
= ((-31 × 2) + (-5)) / 8
= (-62 – 5) / 8
= (-67) / 8
(vi) 5 / 36 and -7 / 12
Solution:
LCM of 36 and 12 is 36
= 5 / 36 + (-7) / 12
= (5 + (-7 × 3)) / 36
= (5 + (-21)) / 36
= (-16) / 36
4 is the common factor that can be canceled
= (-4) / 9
(vii) -5 / 16 and 7 / 24
Solution:
LCM of 16 and 24
16 = 2 × 2 × 2 × 2
24 = 2 × 2 × 2 × 3
LCM = 2 × 2 × 2 × 2 × 3 = 48
= (-5) / 16 + 7 / 24
= ((-5 × 3) + 7 × 2) / 48
= (-15 + 14) / 48
= (-1) / 48
(viii) 7 / -18 and 8 / 27
Solution:
LCM of 18 and 27
18 = 2 × 3 × 3
27 = 3 × 3 × 3
LCM = 3 × 3 × 3 × 2 = 54
= ((-7 × 3) + 8 × 2) / 54
= (-21 + 16) / 54
= (-5) / 54
Question 3. Simplify:
(i) 8 / 9 + -11 / 6
Solution:
LCM of 9 and 6
9 = 3 × 3
6 = 2 × 3
LCM = 2 × 3 × 3 = 18
= (8 × 2 + (-11 × 3)) / 18
= (16 – 33) / 18
= (-17) / 18
(ii) 3 + 5 / -7
LCM of 1 and 7 is 7
= (3 × 7 + (-5)) / 7
= (21 – 5) / 7
= 16 / 7
(iii) 1 / -12 + 2 / -15
Solution:
LCM of 12 and 15
12 = 2 × 2 × 3
15 = 3 × 5
LCM = 2 × 2 × 3 × 5 = 60
= ((-1 × 5) + (-2 × 4)) / 60
= (-5 – 8) / 60
= (-13) / 60
(iv) -8 / 19 + -4 / 57
Solution:
LCM of 19 and 57 is 57
= ((-8 × 3) + (-4)) / 57
= (-24 – 4) / 57
= (-28) / 57
(v) 7 / 9 + 3 / -4
Solution:
LCM of 9 and 4 is 36
= (7 × 4 + (-3 × 9)) / 36
= (28 – 27) / 36
= 1 / 36
(vi) 5 / 26 + 11 / -39
Solution:
LCM of 26 and 39
26 = 13×2
39 = 13×3
LCM = 13 × 2 × 3 = 78
= (5 × 3 + (-11 × 2)) / 78
= (15 – 22) / 78
= (-7) / 78
(vii) -16 / 9 + -5 / 12
Solution:
LCM of 16 and 12
9 = 3×3
12 = 2 × 2 × 3
LCM = 3 × 3 × 2 × 2 = 36
= ((-16 × 4) + (-5 × 3)) / 36
= (-64 – 15) / 36
= (-79) / 36
= (-79) / 36
(viii) -13 / 8 + 5 / 36
Solution:
LCM of 8 and 36
8 = 2 × 2 × 2
36 = 2 × 2 × 3 × 3
LCM = 2 × 2 × 2 × 3 × 3 = 72
= ((-13 × 9) + 5 × 2) / 72
= (-117 + 10) / 72
= (-107) / 72
(ix) 0 + -3 / 5
Solution:
0 is the additive identity, if added to any number gives the same number
= (-3) / 5
(x) 1 + -4 / 5
Solution:
LCM of 1 and 5 is 5
= (1 × 5 + (-4)) / 5
= (5 – 4) / 5
= 1 / 5
Question 4. Add and express the sum as mixed fraction:
(i) -12 / 5 and 43 / 10
Solution:
LCM is 10
= ((-12 × 2 + 43)) / 10
= (-24 + 43) / 10
= 19 / 10
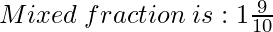
(ii) 24 / 7 and -11 / 4
Solution:
LCM of 7 and 4 is 28
= (24 × 4 + (-11 × 7)) / 28
= (96 – 77) / 28
= 19 / 28
Proper fraction cannot be converted to mixed fraction
(iii) -31 / 6 and -27 / 8
Solution:
LCM of 8 and 6 is 24
= ((-31 × 4) + (-27 × 3)) / 16
= (-124 – 81) / 24
= (-205) / 24
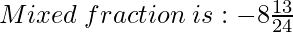
(iv) 101 / 6 and 7 / 8
Solution:
LCM of 8 and 6 is 24
101 / 6 + 7 / 8
= (101 × 4 + 7 × 3) / 24
= (404 + 21) / 24
= 425 / 24
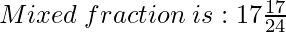
Share your thoughts in the comments
Please Login to comment...