Program to check if a number is divisible by any of its digits
Last Updated :
01 Aug, 2023
Given an integer N where 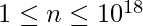 . The task is to check whether the number is not divisible by any of its digit. If the given number N is divisible by any of its digits then print “YES” else print “NO”.
. The task is to check whether the number is not divisible by any of its digit. If the given number N is divisible by any of its digits then print “YES” else print “NO”.
Examples:
Input : N = 5115
Output : YES
Explanation: 5115 is divisible by both 1 and 5.
So print YES.
Input : 27
Output : NO
Explanation: 27 is not divisible by 2 or 7
Approach: The idea to solve the problem is to extract the digits of the number one by one and check if the number is divisible by any of its digit. If it is divisible by any of it’s digit then print YES otherwise print NO.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string isDivisible(long long int n)
{
long long int temp = n;
while (n) {
int k = n % 10;
if (temp % k == 0)
return "YES";
n /= 10;
}
return "NO";
}
int main()
{
long long int n = 9876543;
cout << isDivisible(n);
return 0;
}
|
Java
class GFG
{
static String isDivisible(int n)
{
int temp = n;
while (n > 0)
{
int k = n % 10;
if (temp % k == 0)
{
return "YES";
}
n /= 10;
}
return "NO";
}
public static void main(String[] args)
{
int n = 9876543;
System.out.println(isDivisible(n));
}
}
|
Python3
def isDivisible(n):
temp = n
while(n):
k = n % 10
if(temp % k == 0):
return "YES"
n /= 10;
return "NO"
n = 9876543
print(isDivisible(n))
|
C#
using System;
class GFG
{
static String isDivisible(int n)
{
int temp = n;
while (n > 0)
{
int k = n % 10;
if (temp % k == 0)
{
return "YES";
}
n /= 10;
}
return "NO";
}
public static void Main(String[] args)
{
int n = 9876543;
Console.WriteLine(isDivisible(n));
}
}
|
Javascript
<script>
function isDivisible(n)
{
temp = n;
while (n)
{
k = n % 10;
if (temp % k == 0)
return "YES";
n = Math.floor(n / 10);
}
return "NO";
}
let n = 9876543;
document.write(isDivisible(n));
</script>
|
PHP
<?php
function isDivisible($n)
{
$temp = $n;
while ($n)
{
$k = $n % 10;
if ($temp % $k == 0)
return "YES";
$n = floor($n / 10);
}
return "NO";
}
$n = 9876543;
echo isDivisible($n);
?>
|
Time Complexity: O(log(N))
Auxiliary Space: O(1), since no extra space has been required.
Method #2: Using string:
- We have to convert the given number to string by taking a new variable .
- Traverse the string ,
- Convert character to integer(digit)
- Check if the number is divisible by any of it’s digit then print YES otherwise print NO.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string getResult(int n)
{
string st = to_string(n);
for (int i = 0; i < st.length(); i++)
{
int d = st[i] - 48;
if(n % d == 0)
{
return "Yes";
}
}
return "No";
}
int main()
{
int n = 9876543;
cout<<getResult(n);
}
|
Java
import java.io.*;
class GFG{
static String getResult(int n)
{
String st = Integer.toString(n);
for (int i = 0; i < st.length(); i++)
{
int d = st.charAt(i) - 48;
if(n % d == 0)
{
return "Yes";
}
}
return "No";
}
public static void main(String[] args)
{
int n = 9876543;
System.out.println(getResult(n));
}
}
|
Python3
def getResult(n):
st = str(n)
for i in st:
if(n % int(i) == 0):
return 'Yes'
return 'No'
n = 9876543
print(getResult(n))
|
C#
using System;
public class GFG{
static String getResult(int n)
{
string st = n.ToString();
for (int i = 0; i < st.Length; i++)
{
int d = st[i] - 48;
if(n % d == 0)
{
return "Yes";
}
}
return "No";
}
public static void Main(String[] args)
{
int n = 9876543;
Console.Write(getResult(n));
}
}
|
Javascript
<script>
function getResult(n)
{
let st = n.toString();
for (let i = 0; i < st.length; i++)
{
let d = st[i].charCodeAt(0) - 48;
if(n % d == 0)
{
return "Yes";
}
}
return "No";
}
let n = 9876543;
document.write(getResult(n));
</script>
|
Output:
Yes
Time Complexity: O(n)
Auxiliary Space: O(n)
Approach 3: Stack:
In this approach, we use a stack to store the digits of the given number.
- We push each digit of the number into the stack until the number becomes zero.
- Then, we pop each digit from the stack and check if it divides the original number evenly. If at any point a digit does not divide the original number evenly, we return “NO” from the function. If all the digits divide the original number evenly, we return “YES”.
- The idea behind this approach is that when we push the digits of the number into the stack, they are stored in the reverse order. When we pop them from the stack, we get the digits in the correct order. Therefore, we can easily check if each digit divides the original number evenly.
- This approach has a time complexity of O(log n), where n is the given number. The space complexity is also O(log n), as we need to store the digits of the number in the stack.
Here is the code of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string isDivisible(long long int n)
{
stack<int> digits;
while (n) {
digits.push(n % 10);
n /= 10;
}
while (!digits.empty()) {
int k = digits.top();
digits.pop();
if (n % k == 0)
return "YES";
}
return "NO";
}
int main()
{
long long int n = 9876543;
cout << isDivisible(n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static String isDivisible(long n) {
Stack<Integer> digits = new Stack<>();
while (n != 0) {
digits.push((int)(n % 10));
n /= 10;
}
while (!digits.empty()) {
int k = digits.pop();
if (n % k == 0)
return "YES";
}
return "NO";
}
public static void main(String[] args) {
long n = 9876543;
System.out.println(isDivisible(n));
}
}
|
Python3
def isDivisible(n):
digits = []
while n:
digits.append(n % 10)
n //= 10
for k in reversed(digits):
if k != 0 and n % k == 0:
return "YES"
return "NO"
n = 9876543
print(isDivisible(n))
|
C#
using System;
using System.Collections.Generic;
public class GFG {
public static string IsDivisible(long n)
{
Stack<int> digits = new Stack<int>();
while (n != 0) {
digits.Push((int)(n % 10));
n /= 10;
}
while (digits.Count > 0) {
int k = digits.Pop();
if (n % k == 0)
return "YES";
}
return "NO";
}
public static void Main(string[] args)
{
long n = 9876543;
Console.WriteLine(IsDivisible(n));
}
}
|
Javascript
function isDivisible(n) {
let digits = [];
while (n) {
digits.push(n % 10);
n = Math.floor(n / 10);
}
while (digits.length > 0) {
let k = digits.pop();
if (n % k == 0)
return "YES";
}
return "NO";
}
let n = 9876543;
console.log(isDivisible(n));
|
Output:
YES
Time Complexity: O(log(N))
Auxiliary Space: O(log n), where n is the given number.
Share your thoughts in the comments
Please Login to comment...