Minimum number of 1’s to be replaced in a binary array

Given a binary array arr[] of zero’s and one’s only. The task is to find the minimum number of one’s to be changed to zero such if there exist any index 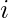in the array such that arr[i] = 0 then arr[i-1] and arr[i+1] both should not be equals to 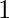at the same time.

That is, for any index 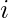the below condition should fail: 

if (arr[i]== 0):
    (arr[i-1] == 1) && (arr[i+1] == 1)

Note: 1-based indexing is considered for the array.

Examples: 

Input : arr[] = { 1, 1, 0, 1, 1, 0, 1, 0, 1, 0 } 
Output : 2 
Explanation: Indexes 2 and 7 OR 4 and 7 can be changed to zero.

Input : arr[] = { 1, 1, 0, 0, 0 } 
Output : 0  

Approach: The idea is that, whenever we found condition like we simply changed the value of (i+1)th index to zero(0). So that index between (i-1)-th and (i+1)-th index is safe.

Below is the implementation of the above approach: 

C++

// C++ program to find minimum number
// of 1's  to be replaced to 0's
#include <bits/stdc++.h>
using namespace std;

// Function to find minimum number
// of 1's  to be replaced to 0's
int minChanges(int A[], int n)
{
    int cnt = 0;

    for (int i = 0; i < n - 2; ++i) {

        if ((i - 1 >= 0) && A[i - 1] == 1
            && A[i + 1] == 1 && A[i] == 0) {
            A[i + 1] = 0;
            cnt++;
        }

    }

    // return final answer
    return cnt;
}

// Driver program
int main()
{
    int A[] = { 1, 1, 0, 1, 1, 0, 1, 0, 1, 0 };
    int n = sizeof(A) / sizeof(A[0]);

    cout << minChanges(A, n);

    return 0;
}

Java

// Java program to find minimum number
// of 1's to be replaced to 0's
import java.lang.*;
import java.util.*;

class GFG
{
// Function to find minimum number
// of 1's to be replaced to 0's
static int minChanges(int[] A, int n)
{
    int cnt = 0;

    for (int i = 0; i < n - 2; ++i)
    {

        if ((i - 1 >= 0) && A[i - 1] == 1 &&
                            A[i + 1] == 1 &&
                            A[i] == 0)
        {
            A[i + 1] = 0;
            cnt++;
        }

    }

    // return final answer
    return cnt;
}

// Driver Code
public static void main(String args[])
{
    int[] A = { 1, 1, 0, 1, 1, 0, 1, 0, 1, 0 };
    int n = A.length;

    System.out.print(minChanges(A, n));
}
}

// This code is contributed
// by Akanksha Rai

Python3

# Python 3 program to find minimum
# number of 1's to be replaced to 0's

# Function to find minimum number
# of 1's to be replaced to 0's
def minChanges(A, n):
    cnt = 0
    for i in range(n - 2):
        if ((i - 1 >= 0) and A[i - 1] == 1 and
           A[i + 1] == 1 and A[i] == 0):
            A[i + 1] = 0
            cnt = cnt + 1

    # return final answer
    return cnt

# Driver Code
A = [1, 1, 0, 1, 1, 0, 1, 0, 1, 0]
n = len(A)
print(minChanges(A, n))

# This code is contributed
# by Shashank_Sharma

C#

// C# program to find minimum number
// of 1's to be replaced to 0's
using System;

class GFG
{
// Function to find minimum number
// of 1's to be replaced to 0's
static int minChanges(int[] A, int n)
{
    int cnt = 0;

    for (int i = 0; i < n - 2; ++i)
    {

        if ((i - 1 >= 0) && A[i - 1] == 1 &&
                            A[i + 1] == 1 && A[i] == 0)
        {
            A[i + 1] = 0;
            cnt++;
        }

    }

    // return final answer
    return cnt;
}

// Driver Code
public static void Main()
{
    int[] A = { 1, 1, 0, 1, 1, 0, 1, 0, 1, 0 };
    int n = A.Length;

    Console.Write(minChanges(A, n));
}
}

// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP program to find minimum number
// of 1's to be replaced to 0's

// Function to find minimum number
// of 1's to be replaced to 0's
function minChanges($A, $n)
{
    $cnt = 0;

    for ($i = 0; $i < $n - 2; ++$i)
    {
        if (($i - 1 >= 0) && $A[$i - 1] == 1 &&
          $A[$i + 1] == 1 && $A[$i] == 0)
        {
            $A[$i + 1] = 0;
            $cnt++;
        }

    }

    // return final answer
    return $cnt;
}

// Driver Code
$A = array(1, 1, 0, 1, 1,
           0, 1, 0, 1, 0);
$n = sizeof($A);

echo minChanges($A, $n);

// This code is contributed
// by Ankita_Saini
?>

Javascript

<script>

// Javascript program to find minimum number
// of 1's  to be replaced to 0's

// Function to find minimum number
// of 1's  to be replaced to 0's
function minChanges(A, n)
{
    var cnt = 0;

    for (var i = 0; i < n - 2; ++i) {

        if ((i - 1 >= 0) && A[i - 1] == 1
            && A[i + 1] == 1 && A[i] == 0) {
            A[i + 1] = 0;
            cnt++;
        }

    }

    // return final answer
    return cnt;
}


var A = [ 1, 1, 0, 1, 1, 0, 1, 0, 1, 0 ];
var n = A.length;
document.write(  minChanges(A, n));


// This code is contributed by SoumikMondal

</script>

Output

2

Complexity Analysis:

• Time Complexity: O(N)
• Auxiliary Space: O(1)