Is every rectangle a rhombus?
Last Updated :
05 Oct, 2021
Rectangle is a two-dimensional geometrical figure depicted by four sides and four corners. A rectangle contains sides such that the length of the opposite sides is equal and these sides are parallel to each other. The sides sharing a corner from adjacent sides with an angle of 90° between them. Therefore, there are four right angles in the rectangle.

Properties of Rectangle
The properties of a rectangle are given below:
- It has four edges and four corners, known as vertices.
- Diagonals of a rectangle bisect each other.
- The area of a rectangle is equivalent to the product of its length and breadth.
- Each vertex has an angle equal to 90o
- The opposite sides of a rectangle are equal and parallel to each other.
- Perimeter is equivalent to twice of sum of its length and breadth.
- Sum of all interior angles equal to 360 degrees
Perimeter of a Rectangle
The total displacement covered by going through the boundary of the rectangle can be termed as the perimeter. Since both length and breadth are denoted by unit length, the perimeter is also measured in unit length.
Perimeter can be denoted by,
Perimeter, P = 2 (Length + Width)
Area of Rectangle
The region covered by a two-dimensional geometrical figure in a plane is called the area of a figure. Thus, the area of a rectangle is the area included within its boundaries. It is measured in square units. The area is equivalent to the product of the length and breadth of the rectangle.
Area can be denoted by,
Area, A = Length × Width sq. units
Diagonal of a Rectangle Formula
Diagonals of any geometrical figure connect alternate vertices. The length of diagonals of a rectangle can be calculated by the following formula, denoted by d,
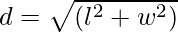
where,
l = length of the rectangle
w = width of the rectangle

Rhombus
A rhombus is also known as a four-sided quadrilateral. It is considered to be a special case of a parallelogram. A rhombus contains parallel opposite sides and equal opposite angles. A rhombus is also known by the name diamond or rhombus diamond. A rhombus contains all the sides of a rhombus as equal in length. Also, the diagonals of a rhombus bisect each other at right angles.

Properties of a Rhombus
A rhombus contains the following properties :
- A rhombus contains all equal sides.
- Diagonals of a rhombus bisect each other at right angles.
- The opposite sides of a rhombus are parallel in nature.
- The sum of two adjacent angles of a rhombus is equal to 180o.
- There is no inscribing circle within a rhombus.
- There is no circumscribing circle around a rhombus.
- The diagonals of a rhombus lead to the formation of four right-angled triangles.
- These triangles are congruent to each other.
- The opposite angles of a rhombus are equal.
- When you connect the midpoint of the sides of a rhombus, a rectangle is formed.
- When the midpoints of half the diagonal are connected, another rhombus is formed.
Perimeter of Rhombus
The perimeter of a rhombus is defined as the total length of its boundaries forming the figure. It can also be denoted as the total summation of the length of four sides of a rhombus. The perimeter of a rhombus is defined by :
Perimeter, P = 4a units
where the diagonals of the rhombus are denoted by d1 & d2 and ‘a’ is the side.
Area of Rhombus
The area of the rhombus is defined as the region enclosed within a two-dimensional plane. The area of a rhombus is equivalent to the product of diagonals of rhombus divided by 2. The area of the rhombus can be defined by the following formula :
Area, A = 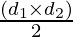 sq. units
sq. units
where d1 and d2 are the diagonals of a rhombus.
We can easily notice that every rhombus is a parallelogram, but the reverse is not true. A square can be considered as a special case of a rhombus since it contains four sides of equal length. A square has all right angles. However, all the angles of a rhombus are not necessarily right angles. Conclusively, a rhombus containing right angles can be considered as a square. Therefore, we can say that,
- All rhombuses are parallelograms.
- All parallelograms are not rhombuses.
- All rhombuses are not squares.
- All squares are rhombuses.

Is every rectangle a Rhombus?
A rectangle is a geometrical figure which doesn’t contain all equal sides. A square is a special case of rectangle with all equal sides. Since, we know, a rhombus has all equal sides. The sets of rectangles and rhombuses only intersect in the case of squares. Therefore, the rectangle is not a rhombus.
Why is a Rhombus a Rectangle?
A rhombus is a special case of a rectangle. Since, we know, that the diagonals of a rhombus intersect at equal angles whereas the diagonals of a rectangle are equal in length. Upon connecting the midpoints of the sides of a rhombus, a rectangle is formed.
Similar Questions
Question 1. Calculate the area of a rectangular frame, which has 6 inches in length and is 3 inches wide.
Solution:
Since, we know,
Area of a Rectangle = (Length × Width) square units.
Substituting the values, we obtain,
the area of rectangular frame = 6 × 3 = 18 square inches
Question 2. Find the length of diagonal of a rectangle which has length as 12 cm and width, 8 cm respectively.
Solution:
We know,
Diagonal Length,
D = 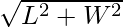
⇒ D = 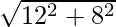
⇒ D = 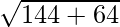
⇒ D = √208
⇒ D = 4√3
Question 3. Find the area of a rhombus with the two diagonal lengths d1 and d2 to be 6cm and 12 cm, respectively.
Solution:
We have,
Diagonal d1 = 6cm
Diagonal d2= 12 cm
Area of the rhombus is given by,
A = 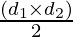 sq. units
sq. units
A = 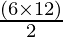
A = 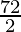
A = 36 cm2
Therefore, the area of rhombus = 36 cm2.
Question 4. Difference between Rhombus and Rectangle?
Solution:
| Property | Rhombus | Rectangle |
| Sides | Equal sides. | Opposite sides are equal. |
| Diagonals |
The diagonals bisect each other at 90°.
Diagonals make right angles at the center.
|
The diagonals bisect each other at different angles. One angle is an obtuse angle and the other one is an acute angle.
Diagonals make different angles at the center – an obtuse angle and an acute angle.
|
| Angles |
Opposite angles are equal.
Adjacent angles add up to 180°.
|
Opposite and adjacent angles are equal.
An angle formed by the adjacent sides of a rectangle is 90°.
|
Share your thoughts in the comments
Please Login to comment...