How to Identify an Algebraic Expression?
Last Updated :
29 Oct, 2021
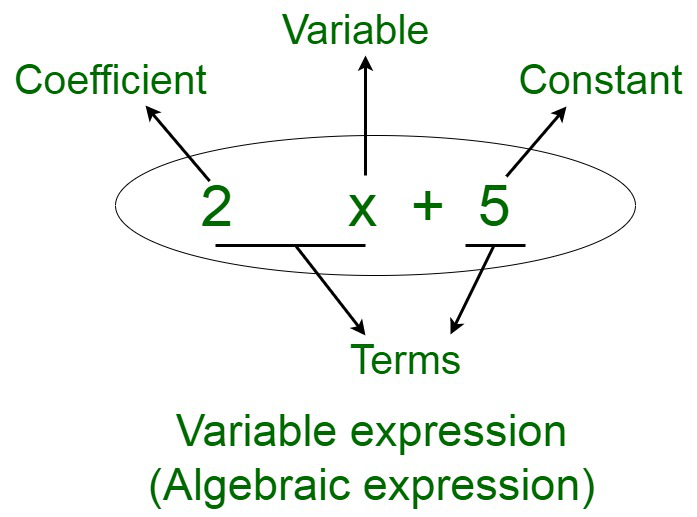
An algebraic expression is an expression composed of various components, such as the variables, constants, coefficients, and arithmetic operations. These components form various parts of the algebraic expressions. An algebraic expression is a linear equation composed of any number of variables. The highest power of the variable is known as the degree. An algebraic expression containing one variable is monomial, two variables is binomial, and so on. For instance, if we assume an expression to be, 2x+5
Terms
The terms of an algebraic expression are known as the components of the expression. An algebraic expression may be composed of one or more terms. A term of an expression may be a constant, a variable, a product of more than two variables (xy), or a product of a variable and a constant. Terms add up together to form an algebraic expression. For instance, in the algebraic expression 3x + y, the two terms are 3x and y. Terms can be further classified depending on the variables and the corresponding powers defining them. They may be divided into like and unlike terms.
Identifying an Algebraic Expression
An algebraic expression is an expression composed of various components or terms. The algebraic expressions may be identified by the following components :
- A variable or a combination of variables – For instance, 4x is an algebraic expression containing x as the variable and 3xy+4 is an algebraic expression containing variables x and y.
- Numbers –
- At least one mathematical operation – Elementary mathematical operations are permissible in the algebraic expression (addition, subtraction, multiplication, or division).
- Algebraic expressions must constitute to a finite sum.
- For instance, let us assume x = 3 . Therefore, for the equation 3x+4 , we have, (3 x 3) + 4 = 13 is obtained. Therefore, 13 is the finite sum obtained.
- Sum of infinite numbers is not an algebraic expression.
- Algebraic expressions must constitute to a finite product.
- Exponents must be either integer or rational in nature.
- For instance, x1/2 is an algebraic expression, whereas xlog 2is not an algebraic expression.
- An algebraic expression may contain integer factorial.
Sample Questions
Question 1: Identify the various components of algebraic expressions: 4x + 3y – 2.
Solution:
The algebraic expression is constituted by the following parts:
4x and 3y, where 4 and 3 are coefficients and x and y, are variables. -2 is the constant part of the expression.
Question 2: Illustrate some types of functions that are not algebraic expressions.
Solution:
Trigonometry and inverse trigonometric functions are functions that are not algebraic in nature. For example, cos x and tan-1 y are not algebraic expressions.
Question 3: Differentiate between algebraic and arithmetic expressions.
Solution:
| Algebraic Expressions | Arithmetic Expressions |
| Can contain variables | Doesn’t contain variables |
| Can contain exponents | Doesn’t contain integer or rational exponents |
Question 4: Solve for x =3, 
Solution:
We have,

for x = 3,
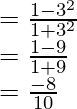
Simplifying,
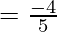
Share your thoughts in the comments
Please Login to comment...