How to find Vertical and Horizontal Asymptotes?

Asymptotes are important in the study of functions as they provide insights into the long-term behaviour of the function and help in understanding its limits as the independent variable approaches certain values or infinity. They are often used in calculus, algebra, and other areas of mathematics to analyze functions and their properties. In this article, we will learn how to find Horizontal and Vertical Asymptotes of any curve.

What are Asymptotes?

Asymptotes are straight lines or curves that a mathematical function approaches but never actually reaches as the independent variable (typically denoted as x) approaches a certain value or infinity.

In other words, an asymptote represents a limit or boundary that a function gets arbitrarily close to but never crosses.

Types of Asymptotes

There are three types of asymptotes in the study of curve sketching i.e.,

• Horizontal Asymptotes
• Vertical Asymptotes
• Oblique (or Slant) Asymptotes

Let’s discuss about these in detail as follows:

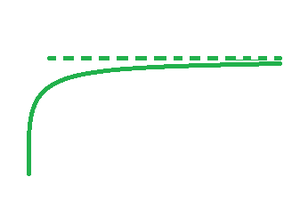
Horizontal Asymptotes

A horizontal asymptote is a horizontal line that shows how a function behaves at the graph’s extreme edges. However, it is quite possible that the function can cross over the asymptote and even touch it. For functions with polynomial numerator and denominator, horizontal asymptotes exist. Rational expressions are the name for these functions. A horizontal form of a function is given as y = k.

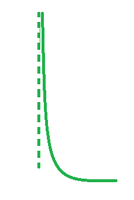
Vertical Asymptotes

A vertical asymptote is a vertical line that directs but does not form part of the graph of a function. The graph will never cross it since it happens at an x-value that is outside the function’s domain. There may be more than one vertical asymptote for a function.

Oblique (or Slant) Asymptotes

Oblique asymptotes occur when the function approaches a straight line with a non-zero slope as x approaches positive or negative infinity. These types of asymptotes typically arise in rational functions where the degree of the numerator is one greater than the degree of the denominator.

Finding Horizontal Asymptotes

In order to calculate the horizontal asymptotes, the point of consideration is the degrees of both the numerator and the denominator of the given function. The criteria for determining the horizontal asymptotes of a function are as follows:

• When the numerator and denominator have the same degree: Divide the coefficients of the leading variables to find the horizontal asymptote.
• If the degree of the numerator is smaller than that of the denominator: The horizontal asymptote is found at y = 0, i.e., the x-axis.
• If the degree of the numerator is greater than that of the denominator: There is no horizontal asymptote for the given rational function.

Finding Vertical Asymptotes

There are two steps to be followed in order to ascertain the vertical asymptote of rational functions. These are:

Step I: Reduce the given rational function as much as possible by taking out any common factors and simplifying the numerator and denominator through factorization.

Step II: Equate the denominator to zero and solve for x. The value(s) of x is the vertical asymptotes of the function.

Read More,

• Curve Tracing
• Rectangular Hyperbola
• Hyperbola

Sample Problems

Problem 1. Find the horizontal and vertical asymptotes of the function: f(x) = [Tex]\frac{x^2-3x}{x+5}  [/Tex].

Solution:

Horizontal Asymptote:

Degree of the numerator = 2

Degree of the denominator = 1

Since the degree of the numerator is greater than that of the denominator, the given function does not have any horizontal asymptote.

Vertical Asymptote:

Since the function is already in its simplest form, just equate the denominator to zero to ascertain the vertical asymptote(s).

⇒ x + 5 = 0

⇒ x = −5

Problem 2. Can a quadratic function have any asymptotes?

Solution:

A quadratic function is a polynomial, so it cannot have any kinds of asymptotes. Since the polynomial functions are defined for all real values of x, it is not possible for a quadratic function to have any vertical asymptotes. Also, since the function tends to infinity as x does, there exists no horizontal asymptote either. 

Problem 3. Find the horizontal and vertical asymptotes of the function: f(x) = [Tex]\frac{3x^2+6x}{x^2+x}  [/Tex].

Solution:

Horizontal Asymptote:

Degree of the numerator = 2

Degree of the denominator = 2

Since the degree of the numerator is equal to that of the denominator, the horizontal asymptote is ascertained by dividing the leading coefficients.

⇒ HA = 2/2 = 1

Vertical Asymptote:

The function needs to be simplified first. [Tex]\frac{3x^2+6x}{x^2+x}=\frac{3x(x+2)}{x(x+1)}=\frac{3(x+2)}{x+1} [/Tex]

Now that the function is in its simplest form, equate the denominator to zero in order to determine the vertical asymptote.

⇒ x + 1 = 0

⇒ x = −1

Problem 4. Find the horizontal and vertical asymptotes of the function: f(x) = 10x² + 6x + 8.

Solution:

The given function is quadratic. A quadratic function is a polynomial, so it cannot have any kinds of asymptotes. Since the polynomial functions are defined for all real values of x, it is not possible for a quadratic function to have any vertical asymptotes. Also, since the function tends to infinity as x does, there exists no horizontal asymptote either. 

Problem 5. Find the horizontal asymptote of the function: f(x) = 9x/x²+2.

Solution:

Degree of numerator = 1

Degree of denominator = 2

Since the degree of the numerator is smaller than that of the denominator, the horizontal asymptote is given by: y = 0.

Problem 6. Find the horizontal and vertical asymptotes of the function: f(x) = x+1/3x-2.

Solution:

Horizontal Asymptote:

Degree of the numerator = 1

Degree of the denominator = 1

Since the degree of the numerator is equal to that of the denominator, the horizontal asymptote is ascertained by dividing the leading coefficients.

⇒ HA = 1/3

Vertical Asymptote:

The function is in its simplest form, equate the denominator to zero in order to determine the vertical asymptote.

⇒ 3x – 2 = 0

⇒ x = 2/3

Problem 7. Find the horizontal and vertical asymptotes of the function: f(x) = x²+1/3x+2.

Solution:

Horizontal Asymptote:

Degree of the numerator = 2

Degree of the denominator = 1

Since the degree of the numerator is greater than that of the denominator, the given function does not have any horizontal asymptote.

Vertical Asymptote:

Since the function is already in its simplest form, just equate the denominator to zero to ascertain the vertical asymtptote(s).

⇒ 3x + 2 = 0

⇒ x = −2/3