How to find the vertex angle?
Last Updated :
29 Nov, 2021
Geometry has been a part of human development from ancient times to the modern world. A glimpse of geometry can be seen in crafts of our ancient architecture. Over time the knowledge of shape and structure has developed way further. In recent times, geometry is a major part of developing infrastructure and it has also made its mark in technological development.
Geometry is a branch of mathematics that deals with the study of shapes, structures, and their properties.
The term geometry originates from the Greek words ‘geo’ which means earth and ‘materia’ which means measurement respectively. A distinct approach for geometrical study and its emphasis can be observed. Geometry is being applicable for constructional development. Along with that, it is also being used in computing designs, blueprints, programming, etc. The given article is a study of part of the geometry that is vertex angle and its properties.
Angle
An angle can be defined as a space between two intersecting lines meeting at a common point. The word is derived from the Latin word ‘angulus’ which means ‘ a corner’. They are measured in a degree that ranges from 0\degree to 360\degree. An angle consists of a common meeting point and two intersecting arms. Angle is a space formed at the meeting point of two intersecting arms. Carpus of Antioch was the first to suppose angle.
Vertex angle
The point at which arms meet and the angle is measured is the angle’s vertex. And the angle measured at the vertex point is called vertex angle. It can be simply defined as a shape or corner formed by two intersecting lines. The figure given shows the vertex point, angle, and intersecting lines.
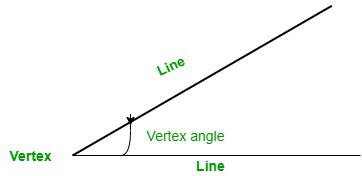
How to find the Vertex angle?
Solution:
It is known that the vertex angle is formed at the vertex. Vertex angles are different for each polygon shape. The angle formula for a regular polygon is given by,
The sum of the interior angles in a regular polygon,
Sum = 180 (n – 2)
For the degree of each interior angle in a regular polygon,
Angle (∠) = 180 (n – 2)/n
Where n = number of sides
List of vertex angles for different shapes
| Name of shape | Vertex angle |
|---|
| Equilateral triangle | 60°
|
| Square | 90°
|
| Pentagon | 108°
|
| Hexagon | 120°
|
| Heptagon | 128.6°
|
| Octagon | 135°
|
| Nonagon | 140°
|
| Decagon | 144°
|
Sample Questions
Question 1: What is the vertex of a circle?
Answer:
A circle consists of constant curvature. Hence, every point in a circle is a vertex.
Question 2: What is the vertex angle of an isosceles triangle?
Answer:
An isosceles triangle has one vertex angle and two congruent base angles. The sum angle is 180 .
.
Question 3: Why is vertex angle important?
Answer:
Vertex angle is important as it helps to define the low point and high point of a shape. For example, it defines the low point of a parabola or high point of an isosceles triangle.
Question 4: What is a common vertex?
Answer:
A common vertex is a point shared by two angles.
Question 5: What is the difference between a corner and a vertex?
Answer:
A corner and vertex are the same as both are defined as the meeting point of two intersecting lines.
Question 6: How many vertexes does a cone have?
Answer:
A cone is a shape with one vertex.
Question 7: List out the number of vertex of different shapes.
Answer:
| Shapes | number of vertices |
|---|
| Cube | 8 vertices |
| Square | 4 vertices |
| Cone | 1 vertex |
| Cylinder | 0 vertex |
| sphere | 0 vertex |
Share your thoughts in the comments
Please Login to comment...