How to find the length of a triangle when given the Perimeter?

In geometry, a triangle is a polygon that has three sides that consist of three edges and three vertices. one of the major properties of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees. This is known as the angle sum property of a triangle. 

What is the Perimeter of a Triangle?

The perimeter of any 2-D figure is defined as the sum of all its side. easily we can calculate it by adding all of its sides. this article contains what is the perimeter, how to find the perimeter of different types of triangles when all side lengths are known. and take examples also that will help you to get more views on the topic.

For any polygon, the sum of all of its sides is known as the perimeter of any figure. In triangles we have,

Perimeter = Sum of the three sides

The unit of perimeter is centimeters(cm), meter(m), it depends on the unit of side.

Perimeter of Triangle Formula

The perimeter of triangle is given by a simple formula, If a, b, c be three sides of triangle , then,

Perimeter, P = a + b + c

where, a, b, and c are sides of the triangle

Properties of Triangle

Every shape has some of its properties that distinguish them from each other. Here are some of the properties of the triangle:

• It has three sides and three angles.
• The sum of all angles of a triangle is always 180 degrees.
• The exterior angles of a triangle always give sum of 360 degrees.
• The consecutive interior and exterior angle is has a sum equal to supplementary.
• The difference between the lengths of any two sides of a triangle is less than the length of the third side, similarly the sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Types of triangles based on sides

Based on the side lengths, triangles are of three types:

• Isosceles triangle
• Scalene triangle
• Equilateral triangle

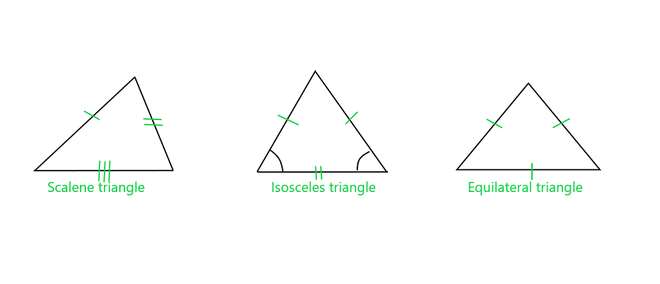
Types of triangles

• Scalene Triangle: It is a type of triangle, in which measures of all the three sides are different, cause in this measure of each angle also differs.
• Isosceles Triangle: In this type of triangle, out of all, two sides have the same length. The two angles opposite to the two equal sides are also equal to each other.
• Equilateral Triangle: In an equilateral triangle all three sides are equal to each other, which leads all the internal angles to be equal, i.e. each of the angles is 60°

Types of Triangles based on Angles

• Acute Angled Triangle: When measures of angle in a triangle are less than 90° then this kind of triangle is an acute angle triangle.
• Right Angled Triangle: When measures of one of the angles is equal to 90° or right angle, then this kind is a right-angled triangle.
• Obtuse Angled Triangle: When the measure of any one angle of the triangle is more than 90°, then this is an obtuse angle triangle.

Perimeter of Right Triangle

A right-angled triangle has Base(b), Perpendicular(p), Hypotenuse(h), using Pythagoras theorem, we have:

h² = b² + p²

and perimeter = h + b+ p

If the perimeter of a triangle is given let say P, then we need to find the length of the side.

Answer:

The answer depends on type triangle is asked, so there are three cases that came into picture,

I case: 

if triangle is Isosceles (two sides are equal let say(a=b)),

then P = a+ b+ c    = 2a + c

II case:

if triangle is scalene (all sides are unequal)

then, P = a+ b+ c

III case:

if triangle is equilateral (all sides are equal)

then, P = a+ a+ a

         P = 3a 

   a = P/3 

Sample Problems

Question 1: Let the length of the Isosceles triangle be x and y calculate perimeter. (assume that two are x)

Solution: 

Perimeter = sum of all sides

P = 2x + y

Question 2: Calculate the perimeter of a triangle if two sides are equal to 12cm and the other 4cm.

Solution:

Perimeter of triangle = sum of all side

P = 12 + 12 + 4 = 28cm.

Question 3: If the perimeter of an equilateral triangle is 27cm, calculate its side.

Answer:

Perimeter of Equilateral triangle = 3 × side 

3 × side = 27

side = 27/3 = 9 cm

Question 4: If the sides i.e., legs of a right triangle are 3cm and 4 cm respectively, then the perimeter is

Solution:

For hypotenuse of triangle, 

h² = b² + p²

h² = 3² + 4²

h = √9 + 16 = √25 = 5

therefore,

perimeter = h+ b+ p

                = 3 + 4 + 5 = 12cm

Question 5: The perimeter of an isosceles triangle is 100 cm. If the base is 36 cm, find the length of the equal sides.

Solution:

Let the length (equal side) be x.

perimeter = l + b + h

∴ x + x + 36 = 100

                2x = 64 

                 x = 32cm.

Question 6: Find the area of the right-angled triangle whose hypotenuse is 15 cm and one of the sides is 12 cm.

Solution:  

AB² = AC² – BC²  

      = 15² – 12²  

      = 225 – 144

       = 81

Therefore, AB = 9

Therefore, area of the triangle = ¹/₂ × base × height

                                                = ¹/₂ × 12 × 9                                               

                                               = 54 cm²

Question 7: The three sides of a triangle are as 5m, 6m and 7m, and then what is the area of the given triangle.

Solution:

Given sides of triangle are 5m, 6m and 7m

s = (5+6+7)/2

Area = √s(s-a)(s-b)(s-c)

        = √9 x 4 x 3 x 2 = 6√6 m².