How to find the altitude of an equilateral triangle given the perimeter?
Last Updated :
09 Nov, 2021
An equilateral triangle is a geometrical 2D figure which has all three sides equal. All the edges subtend an angle of 60° at the corners. Therefore, the sum of all the angles of the triangle is 180°.

Properties of an equilateral triangle
- All three sides of an equilateral triangle are equal.
- All the three angles are equal i.e 60° each.
- A regular polygon has three equal sides.
Perimeter of an Equilateral Triangle
The perimeter of a square is referred to as the total length of the boundary enclosing the geometrical figure.
Perimeter of equilateral triangle = Sum of all sides of an equilateral triangle
Let us assume a to be the side of an equilateral triangle.
Since, we know, all the sides of the equilateral triangle are equal.
Perimeter of equilateral triangle = a + a + a
Perimeter of equilateral triangle = 3a
Altitude of an equilateral triangle
Perimeter of an equilateral triangle can be calculated using the altitude of the triangle.
Let us assume ‘a’ to be the side of an equilateral triangle.
Since,
Height of an Equilateral Triangle = 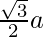
Now, let us assume P to be the perimeter of the equilateral triangle.
P = side + side + side
Since, all the sides are equal,
P = 3a
Substituting values,
Height = 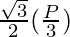
Sample Questions
Question 1. Calculate the perimeter of an equilateral triangle having a height 20√3 cm.
Solution:
Here we have to find the Perimeter of the equilateral triangle with the height 20√3 cm
Formula for calculating perimeter using height is given below
Height = 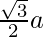
Here a is the side of the equilateral triangle
20√3 = 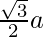
a = 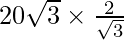
a = 40 cm
Now further finding perimeter of the equilateral triangle
Perimeter of equilateral triangle = side + side + side = 3a
Perimeter of equilateral triangle = 3 × 40
Perimeter of equilateral triangle = 120 cm
Question 2. Assume the height of an Equilateral triangle is 100√3 m, then find its perimeter?
Solution:
Here we have to find the Perimeter of the equilateral triangle with the height 100√3 m
Formula for calculating perimeter using height is given below
Height = 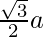
Here a is the side of the equilateral triangle
100√3 = 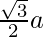
a = 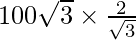
a = 200 m
Now further finding perimeter of the equilateral triangle
Perimeter of equilateral triangle = side + side + side = 3a
Perimeter of equilateral triangle = 3 × 200
Perimeter of equilateral triangle = 600 m
Question 3. Find the perimeter of an equilateral triangle with each side 22 m. Also, find its height?
Solution:
First find the perimeter of an equilateral triangle
Perimeter of equilateral triangle = side + side + side = 3a
Perimeter of equilateral triangle = 3 × 22
Perimeter of equilateral triangle = 66 m
Further finding the height of the equilateral triangle
Height = 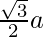
Here a is side of the equilateral triangle
Height = 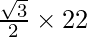
Height of the equilateral triangle = 11√3
Question 4. If the perimeter of an equilateral triangle is 99 cm, then find the height of the equilateral triangle?
Solution:
First we have to find the side of equilateral triangle
As we know that
Perimeter of equilateral triangle = side + side + side = 3a
As given in the question
Perimeter of equilateral triangle = 99 cm
3a = 99 cm
a = 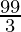
a = 33 cm
Hence the side of triangle is 33 cm
Further finding the height of the equilateral triangle
Height = 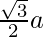
Here a is side of the equilateral triangle
Height = 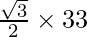
Height of the equilateral triangle = 16.5√3
Question 5. Find out the perimeter of an equilateral triangle having a height of 200 cm.
Solution:
Here we have to find the Perimeter of the equilateral triangle with the height 200 cm
Formula for calculating perimeter using height is given below
Height = 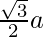
Here a is the side of the equilateral triangle
200 = 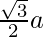
a = 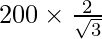
a = 230.94 cm
Now further finding perimeter of the equilateral triangle
Perimeter of equilateral triangle = side + side + side = 3a
Perimeter of equilateral triangle = 3 × 230.94
Perimeter of equilateral triangle = 692.82 cm
Share your thoughts in the comments
Please Login to comment...