How to Find Correlation Coefficient in Excel?
Last Updated :
19 Mar, 2024
Correlation basically means a mutual connection between two or more sets of data. In statistics, bivariate data or two random variables are used to find the correlation between them. The correlation coefficient is generally the measurement of the correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.
If the correlation coefficient is 0, the bivariate data are not correlated with each other.
If the correlation coefficient is -1 or +1, the bivariate data are strongly correlated with each other.
r=-1 denotes strong negative relationship and r=1 denotes strong positive relationship.
In general, if the correlation coefficient is close to -1 or +1 then we can say that the bivariate data are strongly correlated to each other.
The correlation coefficient is calculated using Pearson’s Correlation Coefficient which is given by :
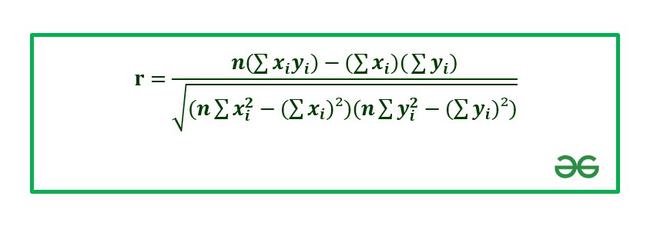
Correlation Coefficient
Where,
- r: Correlation coefficient.
- [Tex] [/Tex]: Values of the variable x.
- y_i: Values of the variable y.
- n: Number of samples taken in the data set.
- Numerator: Covariance of x and y.
- Denominator: Product of Standard Deviation of x and Standard Deviation of y.
In this article, we are going to see how to find correlation coefficients in Excel.
Example: Consider the following data set :

Finding the Correlation Coefficient in Excel:
1. Using CORREL function
In Excel to find the correlation coefficient use the formula :
=CORREL(array1,array2)
array1 : array of variable x
array2: array of variable y
To insert array1 and array2 just select the cell range for both.
1. Let’s find the correlation coefficient for the variables and X and Y1.
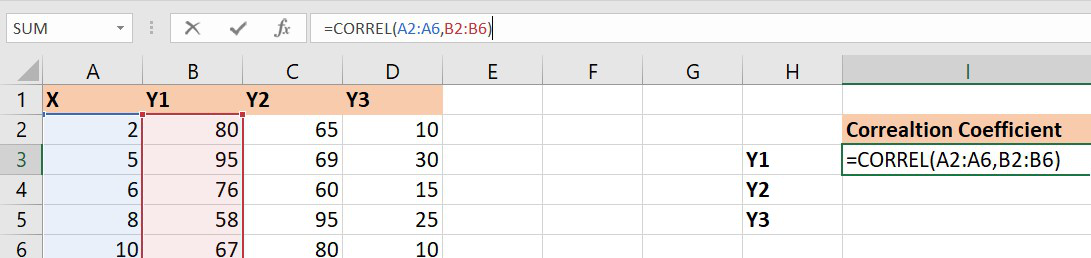
Correlation coefficient of x and y1
array1 : Set of values of X. The cell range is from A2 to A6.
array2 : Set of values of Y1. The cell range is from B2 to B6.
Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula. Finally, the correlation coefficients are as follows :

From the above table we can infer that :
X and Y1 have negative correlation coefficient.
X and Y2 have positive correlation coefficient.
X and Y3 are not correlated as the correlation coefficient is almost zero.
Example: Now, let’s proceed to the further two methods using a new data set. Consider the following data set :

Using Data Analysis
We can also analyze the given dataset and calculate the correlation coefficient: To do so follow the below steps:
Step 1: First you need to enable Data Analysis ToolPak in Excel. To enable :
- Go to File tab in the top left corner of the Excel window and choose Options.
- The Excel Options dialog box opens. Now go to the Add-Ins option and in the Manage select Excel Add-ins from the drop down.
- Click on Go button.
- The Add-ins dialog box opens. In this check the option Analysis ToolPak.
- Click OK!


Data Analysis tab added
Step 2: Now click on Data followed by Data Analysis. A dialog box will appear.
Step 3: In the dialog box select Correlation from the list of options. Click OK!

Step 4: The Correlation menu will appear.
Step 5: In this menu first provide the Input Range. The input range is the cell range of X and Y1 columns as highlighted in the picture below.
Step 6: Also, supply the Output Range as the cell number where you want to display the result. By default, the output will appear in the new Excel sheet in case if you don’t provide any Output Range.
Step 7: Check the Labels in first-row option if you have labels in the dataset. In our case column 1 has label X and column 2 has label Y1.
Step 8: Click OK.

Step 9: The Data Analysis table is now ready. Here, you can see the correlation coefficient between X and Y1 in the analysis table.

Similarly, you can find correlation coefficients of XY2 and that of XY3. Finally, all the correlation coefficients are :

Using PEARSON Function
It is exactly similar to the CORREL function which we have discussed in the above section. The syntax for PEARSON function is :
=PEARSON(array1,array2)
array1 : array of variable x
array2: array of variable y
To insert array1 and array2 just select the cell range for both.
Let’s find the correlation coefficient for X and Y1 in the data set of Example 2 using PEARSON function.
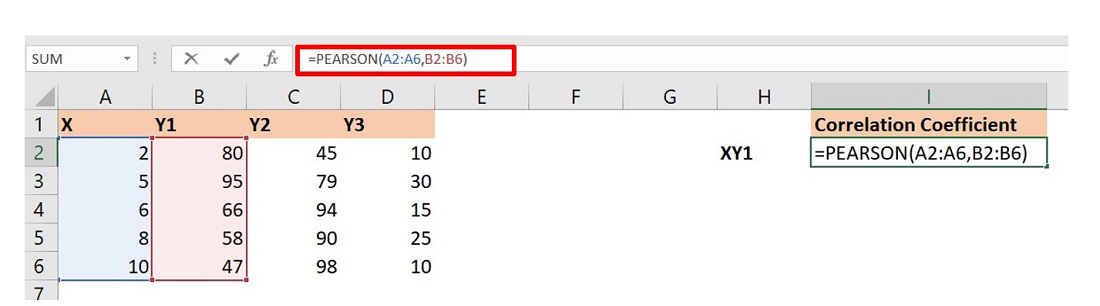
The formula will return the correlation coefficient of X and Y1. Similarly, you can do for others.
The final correlation coefficients are :

Share your thoughts in the comments
Please Login to comment...