Arithmetic probably has the longest history during the time. It is a method of calculation that is been in use from ancient times for normal calculations like measurements, labeling, and all sorts of day-to-day calculations to obtain definite values. The term got originated from the Greek word “arithmos” which simply means numbers.
Arithmetic is the elementary branch of mathematics that specifically deals with the study of numbers and properties of traditional operations like addition, subtraction, multiplication, and division.
Besides the traditional operations of addition, subtraction, multiplication, and division arithmetic also include advanced computing of percentage, logarithm, exponentiation and square roots, etc. Arithmetic is a branch of mathematics concern with numerals and their traditional operations.
History of Arithmetics
Arithmetics have the longest in the field of mathematics. It is in use since the ancient times of human civilization. It was initially used to find the sum and difference of objects as well as for monetization purposes.
- The 17th-century Indian mathematician Brahmagupta is the “father of arithmetic”
- Carl Friedrich Gauss in 1801, provided the Fundamental principle of number theory.
What is Arithmetic Mean?
Arithmetic mean is defined as the sum of all of the numbers of the group, when divided by the number of items present in it.
Arithmetic mean is simply also known as mean or average. The symbol used for the arithmetic mean is ‘X’. It is a method to calculate central tendency. It can simply be understood as a single average value obtained by the calculation of entire data.
Arithmetic is useful in day-to-day calculation as it gives a definite value, as well as it is easy to calculate and understand as it is based on observations. Whereas, as there are also some cases that give an absurd value which counts as a demerit.
The formula of arithmetic mean is given by:
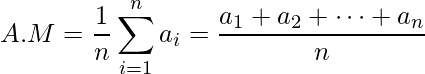
Where,
- N is the number of items
- A.M is the arithmetic mean
- ai is set values
Now, let’s jump into the question.
How to find the Arithmetic Mean?
We can calculate the arithmetic mean by summing up all the numbers of the group and dividing the sum by the number of items.
Its mathematical representation can be shown as-
X = Sum of Values/N
Where
X is the arithmetic mean
N is the number of items
For example, the arithmetic mean of the numbers 2, 3, 4, and 7 will be given by
X = (2 + 3 + 4 + 7)/4
= 16/4 = 4
Sample Questions
Question 1:The marks obtained in math by 4 students of the class are 10,12, 22, and 30. Find its arithmetic mean.
Solution:
As we know,
A.M = Sum of all numbers/Total no. of items
A.M = (10 + 12 + 22 + 28)/4
= 72/4 = 51
Therefore, the mean is 51.
Question 2: If the arithmetic means of 5 observations 6, 7, 5, x, 10 is 6. Find the value of x.
Solution:
Given,
The 5 observations are 6, 7, 5, x, 10
no. of items (n) = 5
Arithmetic mean = 6
We have,
X = Sum of all numbers/Total no. of items
=>6 = (6 + 7 + 5 + x + 10)/5
=>30 = 28 + x
=>x = 30 – 28 = 2
Therefore, the value of missing observation is 2.
Question 3: If the arithmetic mean of 2a+3, a+2, 3a+4, 4a+5 is a+2, find the value of a.
Solution:
Given,
The observations are 2a+3, a+2, 3a+4 and 4a+5.
hence, no. of items (n) = 4
Arithmetic mean (X) = a + 2
We have,
X = Sum of all numbers/Total no. of items
=>X = [(2a + 3) + (a + 2) + (3a + 4) + (4a + 5)/4
=>a + 2 = (10a + 14)/4
=>4(a + 2) = (10a + 14)
=>4a + 8 = 10a + 14
=>(-6a) = (-6)
=>a = -1
Therefore, the value of a is -1.
Question 4: The marks obtained by Subham in terminal examinations are 50, 35, 40, 45, and 55 respectively. Calculate the arithmetic mean.
Solution:
Given,
The observations are 50, 35, 40,45, and 55.
No. of items (n) = 5
Arithmetic mean(X) = ?
We have,
X = Sum of all numbers/ Total no. of items
=>X = (50 + 35 + 40 + 45 + 55)/5
=>X = 225/5
=>X = 225/5 = 45
Therefore, the arithmetic mean of marks obtained is 45.
Question 5: Find the mean of the first five prime numbers.
Solution:
The first five prime numbers are 2, 3, 5, 7 and 11.
No. of observations (n) = 5
We have,
X = Sum of all numbers/ No. of items
=>X = (2 + 3 + 5 + 7 + 11)/5
=>X = 28/5 = 5.6
Therefore, the arithmetic mean of the first five prime numbers is 5.6.
Question 6: The arithmetic mean of five observations m, m+4, m+6, m+8, and m+12 is 16. Find the value of m.
Solution:
Given,
The observations are m, m+4, m+6, m+8 and m+12.
No. of items (n) = 5
Arithmetic mean (X) = 16
We have,
X=sum of all numbers/no. of items
=>X = [m + (m + 4) + (m + 6) + (m + 8) + (m + 12)]/5
=>16 = (5m + 30)/5
=>80 = 5m + 30
=>5a = 50
=>m = 10
Therefore, the value of m is 10.
Share your thoughts in the comments
Please Login to comment...