How to convert a complex number to exponential form?

Complex numbers are a way of numerical representation in the form of a + ib in which a and b stands for real numbers and stands for imaginary number. For example, 2 + 5i is a complex number in which 2 and 5 are the real numbers in the place of a and b. And, i is the imaginary number.

Different forms of a complex number

Complex numbers are divided into three forms that are rectangular form, polar form, and exponential form. Among these three general forms or rectangular form is taken as the standard and easiest way to represent a complex number. If one wants to change the form of the complex number from rectangular to any other form. Firstly, determine the r and θ of the modulus.

The three different forms to represent a complex number are mentioned below with their mathematical representation.

• Rectangular form

z = a + ib

• Polar form

z = r(cosθ + isinθ)

• Exponential form

z = r exp(iθ)

Classification of complex numbers

The complex numbers are classified into different groups on the grounds of the real and imaginary parts of the number. On the basis of standard complex number form, z = a + ib complex numbers are classified into four types.

• Zero complex numbers

a = 0 and b = 0

The form of a complex number will be 0 + i0.

For example 0 (zero)

• Purely real number

a ≠ 0 and b = 0

The form of a complex number will be a.

For example 2, 3, 7, etc

• Purely imaginary number

a = 0 and b ≠ 0

The form of a complex number will be ib.

For example: -7i, -5i, 3i, etc

• Imaginary numbers

a ≠ 0 and b ≠ 0

The form of a complex number will be a+ib.

For example: (-1 – i), (1 + i), (1 – i) etc

How to convert a complex number to exponential form?

Solution:

If there is a complex number in polar form z = r(cosθ + isinθ), use Euler’s formula to write it into an exponential form that is z = re^(iθ). Let’s take a look at the derivation,

Derivation of exponential form

• The exponential form of a complex number can be written as

z = re^iθ

• Complex number in polar form is written as

z = r(cosθ + isinθ)

• Now, we have Euler’s formula

e^iθ = cosθ + isinθ

• Using Euler’s formula we can replace the cosθ + isinθ in an e^iθ to obtain the exponential form of a complex number.

z = r(cosθ + isinθ)

z = re^iθ

Sample problems

Question 1: Convert the complex number 2 + 3i into exponential form.

Solution:

r = 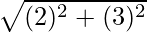=√13

θ = tan^-1(3/2) = 0.982radians

In the exponential form,

re^iθ = √13e^0.982i

Question 2: Convert the complex number 16 + 51i into exponential form.

Solution:

r = 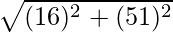= 53.45

θ = arctan(51/16) = 1.27radians

In the exponential form,

re^iθ = 53.45e^1.27i

Question 3: Convert the complex number 12 + 87i into exponential form.

Solution:

r = 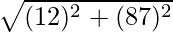= 87.82

θ = arctan(87/12) = 1.43radians

In the exponential form,

re^iθ = 87.82e^1.43i