Find if an undirected graph contains an independent set of a given size
Last Updated :
06 Sep, 2022
Given an undirected graph, check if it contains an independent set of size k. Print ‘Yes’ if there exists an independent set of size k. Print ‘No’ otherwise.
Independent Set: An independent set in a graph is a set of vertices that are not directly connected to each other.
Example 1:
Input : K = 4,
graph = [[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1]]
Output : Yes 
The above graph contains an independent set of size 4 (vertices 1, 2, 3, 4 are not directly connected to each other). Hence, the output is ‘Yes’.
Example 2:
Input : K = 4,
graph = [[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 1],
[0, 1, 0, 1, 1]]
Output : No
The above graph doesn’t contain an independent set of size 4. Hence, the output is ‘No’.
Approach:
- Initialize a variable sol with boolean False value.
- Find all the possible sets of vertices of size K from the given graph.
- If an independent set of size k is found, change the value of sol to True and return.
- Else continue checking for other possible sets.
- In the end, if sol is True, print ‘Yes’ else print ‘No’.
Below is the implementation of the above approach:
C++14
#include <bits/stdc++.h>
using namespace std;
bool check(int[][5], vector<int> &, int);
bool func(int graph[][5], vector<int> &arr,
int k, int index, bool sol[])
{
if (k == 0)
{
if (check(graph, arr, arr.size()))
{
sol[0] = true;
return true;
}
}
else
{
if (index >= k)
{
vector<int> newvec(arr.begin(), arr.end());
newvec.push_back(index);
return (func(graph, newvec, k - 1,
index - 1, sol) or
func(graph, arr, k, index - 1, sol));
}
else
{
arr.push_back(index);
return func(graph, arr, k - 1,
index - 1, sol);
}
}
}
bool check(int graph[][5], vector<int> &arr, int n)
{
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
if (graph[arr[i]][arr[j]] == 1)
return false;
return true;
}
int main()
{
int graph[][5] = {{1, 1, 0, 0, 0},
{1, 1, 1, 1, 1},
{0, 1, 1, 0, 0},
{0, 1, 0, 1, 0},
{0, 1, 0, 0, 1}};
int k = 4;
vector<int> arr;
bool sol[] = {false};
int n = sizeof(graph) /
sizeof(graph[0]);
func(graph, arr, k, n - 1, sol);
if (sol[0])
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static Vector<Integer> arr =
new Vector<>();
static boolean func(int graph[][],
int k, int index,
boolean sol[])
{
if (k == 0)
{
if (check(graph,
arr.size()))
{
sol[0] = true;
return true;
}
}
else
{
if (index >= k)
{
Vector<Integer> newvec =
new Vector<>();
newvec.add(index);
return (func(graph, k - 1,
index - 1, sol) ||
func(graph, k,
index - 1, sol));
}
else
{
arr.add(index);
return func(graph, k - 1,
index - 1, sol);
}
}
return true;
}
static boolean check(int graph[][],
int n)
{
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
if (graph[arr.get(i)][arr.get(j)] == 1)
return false;
return true;
}
public static void main(String[] args)
{
int graph[][] = {{1, 1, 0, 0, 0},
{1, 1, 1, 1, 1},
{0, 1, 1, 0, 0},
{0, 1, 0, 1, 0},
{0, 1, 0, 0, 1}};
int k = 4;
boolean []sol = new boolean[1];
int n = graph.length;
func(graph, k, n - 1, sol);
if (sol[0])
System.out.print("Yes" + "\n");
else
System.out.print("No" + "\n");
}
}
|
Python3
def func(graph, arr, k, index, sol):
if k == 0:
if check(graph, arr) == True:
sol[0] = True
return
else:
if index >= k:
return (func(graph, arr[:] + [index], k-1, index-1, sol) or
func(graph, arr[:], k, index-1, sol))
else:
return func(graph, arr[:] + [index], k-1, index-1, sol)
def check(graph, arr):
for i in range(len(arr)):
for j in range(i + 1, len(arr)):
if graph[arr[i]][arr[j]] == 1:
return False
return True
graph = [[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1]]
k = 4
arr = []
sol = [False]
func(graph, arr[:], k, len(graph)-1, sol)
if sol[0] == True:
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG{
static List<int> arr = new List<int>();
static bool func(int [,]graph,
int k, int index,
bool []sol)
{
if (k == 0)
{
if (check(graph,
arr.Count))
{
sol[0] = true;
return true;
}
}
else
{
if (index >= k)
{
List<int> newvec = new List<int>();
newvec.Add(index);
return (func(graph, k - 1,
index - 1, sol) ||
func(graph, k,
index - 1, sol));
}
else
{
arr.Add(index);
return func(graph, k - 1,
index - 1, sol);
}
}
return true;
}
static bool check(int [,]graph, int n)
{
for(int i = 0; i < n; i++)
for(int j = i + 1; j < n; j++)
if (graph[arr[i],arr[j]] == 1)
return false;
return true;
}
public static void Main(String[] args)
{
int [,]graph = { { 1, 1, 0, 0, 0 },
{ 1, 1, 1, 1, 1 },
{ 0, 1, 1, 0, 0 },
{ 0, 1, 0, 1, 0 },
{ 0, 1, 0, 0, 1 } };
int k = 4;
bool []sol = new bool[1];
int n = graph.GetLength(0);
func(graph, k, n - 1, sol);
if (sol[0])
Console.Write("Yes" + "\n");
else
Console.Write("No" + "\n");
}
}
|
Javascript
<script>
function func(graph, arr,k, index, sol)
{
if (k == 0)
{
if (check(graph, arr, arr.length))
{
sol[0] = true;
return true;
}
}
else
{
if (index >= k)
{
let newvec = new Array();
for(let x of arr){
newvec.push(x);
}
newvec.push(index);
return (func(graph, newvec, k - 1,index - 1, sol) || func(graph, arr, k, index - 1, sol));
}
else
{
arr.push(index);
return func(graph, arr, k - 1,index - 1, sol);
}
}
}
function check(graph,arr,n)
{
for (let i = 0; i < n; i++)
for (let j = i + 1; j < n; j++)
if (graph[arr[i]][arr[j]] == 1)
return false;
return true;
}
let graph = [[1, 1, 0, 0, 0],
[1, 1, 1, 1, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1]];
let k = 4;
let arr = [];
let sol = [false];
let n = graph.length;
func(graph, arr, k, n - 1, sol);
if (sol[0])
document.write("Yes");
else
document.write("No");
</script>
|
Complexity Analysis:
- Time Complexity:
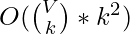 where V is the number of vertices in the graph and k is the given size of set.
where V is the number of vertices in the graph and k is the given size of set. - Auxiliary Space: O(V)
Share your thoughts in the comments
Please Login to comment...