Find all good indices in the given Array
Last Updated :
08 Sep, 2022
Given an array A[] of integers. The task is to print all indices 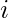 of this array such that after removing the ith element from the array, the array becomes a good array.
of this array such that after removing the ith element from the array, the array becomes a good array.
Note:
- An array is good if there is an element in the array that equals to the sum of all other elements.
- 1-based indexing is considered for the array.
Examples:
Input : A[] = { 8, 3, 5, 2 }
Output : 1 4
Explanation: A[] = [8, 3, 5, 2]
If you remove A[1], the array will look like [3, 5, 2] and it is good, since 5 = 3+2.
If you remove A[4], the array will look like [8, 3, 5] and it is good, since 8 = 3+5.
Hence the nice indices are 1 and 4.
Input : A[] = { 2, 2, 2 }
Output : 1 2 3
Removing any element at any indices will make array good.
Approach:
- Create a hash of array A[] which store frequency of each element and a variable sum having sum of each element of A.
- Iterate the array, remove the element at index i for each
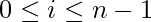 .
. - After removing an element the sum of remaining array is K, where K = sum – A[i].
- We have to find an element K/2 in the remaining array to make it good. Let K = K/2 for now.
- Now the remaining array will be good if and only if below conditions holds true.
- If A[i] == K and hash(K) > 1 OR If A[i] != K and hash(K) > 0.
- Print all such indices i.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void niceIndices(int A[], int n)
{
int sum = 0;
map<int, int> m;
for (int i = 0; i < n; ++i) {
m[A[i]]++;
sum += A[i];
}
for (int i = 0; i < n; ++i) {
int k = sum - A[i];
if (k % 2 == 0) {
k = k >> 1;
if (m.find(k) != m.end()) {
if ((A[i] == k && m[k] > 1) || (A[i] != k))
cout << (i + 1) << " ";
}
}
}
}
int main()
{
int A[] = { 8, 3, 5, 2 };
int n = sizeof(A) / sizeof(A[0]);
niceIndices(A, n);
return 0;
}
|
Java
import java.util.*;
class Solution
{
static void niceIndices(int A[], int n)
{
int sum = 0;
Map<Integer, Integer> m=new HashMap<Integer, Integer>();
for (int i = 0; i < n; ++i) {
m.put(A[i],(m.get(A[i])==null)?0:m.get(A[i])+1);
sum += A[i];
}
for (int i = 0; i < n; ++i) {
int k = sum - A[i];
if (k % 2 == 0) {
k = k >> 1;
if (m.containsKey(k)) {
if ((A[i] == k && m.get(k) > 1) || (A[i] != k))
System.out.print( (i + 1) +" ");
}
}
}
}
public static void main(String args[])
{
int A[] = { 8, 3, 5, 2 };
int n = A.length;
niceIndices(A, n);
}
}
|
Python3
from collections import defaultdict
def niceIndices(A, n):
Sum = 0
m = defaultdict(lambda:0)
for i in range(n):
m[A[i]] += 1
Sum += A[i]
for i in range(n):
k = Sum - A[i]
if k % 2 == 0:
k = k >> 1
if k in m:
if ((A[i] == k and m[k] > 1) or
(A[i] != k)):
print((i + 1), end = " ")
if __name__ == "__main__":
A = [8, 3, 5, 2]
n = len(A)
niceIndices(A, n)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void niceIndices(int []A, int n)
{
int sum = 0;
Dictionary<int,int> mp = new Dictionary<int,int>();
for (int i = 0 ; i < n; i++)
{
if(mp.ContainsKey(A[i]))
{
var val = mp[A[i]];
mp.Remove(A[i]);
mp.Add(A[i], val + 1);
sum += A[i];
}
else
{
mp.Add(A[i], 0);
sum += A[i];
}
}
for (int i = 0; i < n; ++i)
{
int k = sum - A[i];
if (k % 2 == 0)
{
k = k >> 1;
if (mp.ContainsKey(k))
{
if ((A[i] == k && mp[k] > 1) || (A[i] != k))
Console.Write( (i + 1) +" ");
}
}
}
}
public static void Main(String []args)
{
int []A = { 8, 3, 5, 2 };
int n = A.Length;
niceIndices(A, n);
}
}
|
Javascript
<script>
function niceIndices(A, n)
{
var sum = 0;
var m = new Map();
for (var i = 0; i < n; ++i) {
if(m.has(A[i]))
m.set(A[i], m.get(A[i])+1)
else
m.set(A[i], 1)
sum += A[i];
}
for (var i = 0; i < n; ++i) {
var k = sum - A[i];
if (k % 2 == 0) {
k = k >> 1;
if (m.has(k)) {
if ((A[i] == k && m.get(k) > 1) || (A[i] != k))
document.write(i + 1 + " ");
}
}
}
}
var A = [8, 3, 5, 2];
var n = A.length;
niceIndices(A, n);
</script>
|
Complexity Analysis:
- Time Complexity: O(N*log(N))
- Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...