In computational geometry, a convex hull is the smallest convex polygon that contains a given set of points. It is a fundamental concept with applications in various fields such as computer graphics, robotics, and image processing.
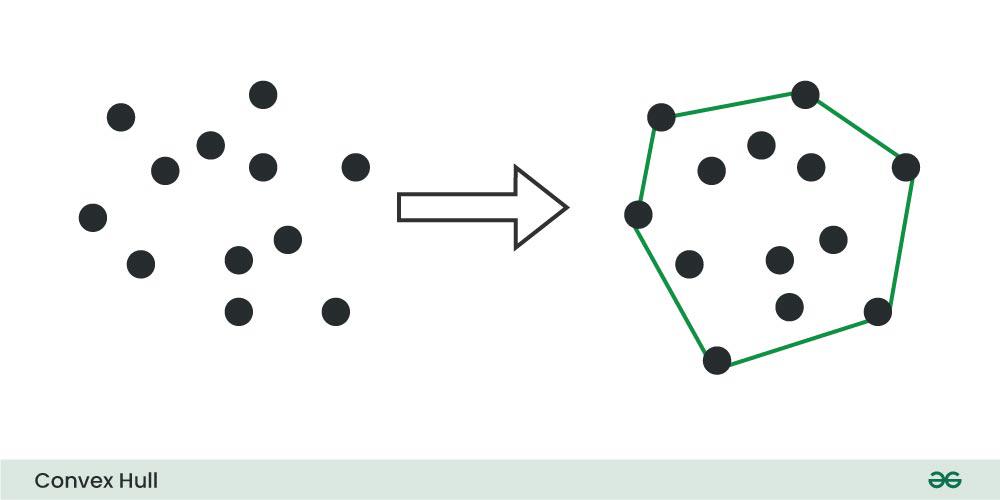
Importance of Convex Hull:
Convex hulls are important in computational geometry for several reasons:
- Collision detection: Convex hulls can be used to efficiently detect collisions between objects in 2D or 3D space.
- Image processing: Convex hulls can be used to extract meaningful shapes from images, such as the outline of an object.
- Data visualization: Convex hulls can be used to visualize the distribution of data points in a scatter plot.
- Input is an array of points specified by their x and y coordinates. The output is the convex hull of this set of points.
Convex Hull using Divide and Conquer Algorithm:
Pre-requisite: Tangents between two convex polygons
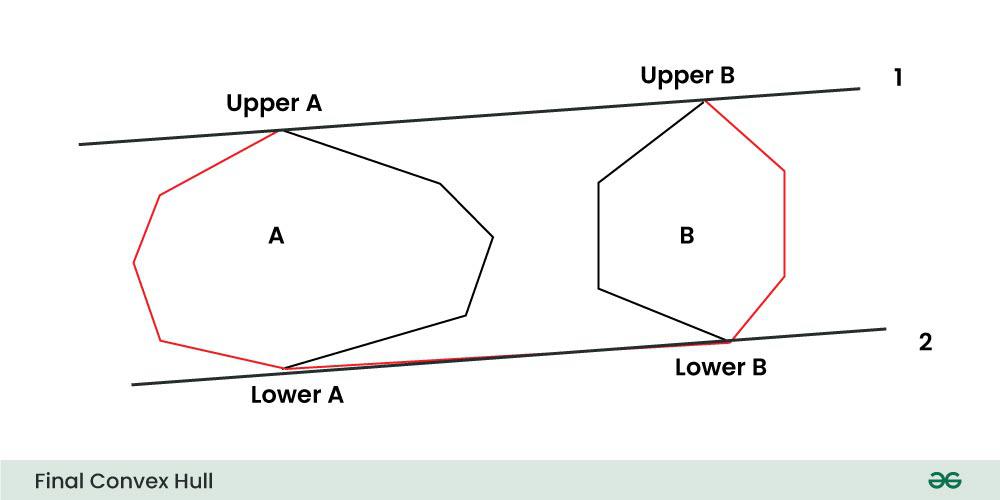
Algorithm: Given the set of points for which we have to find the convex hull. Suppose we know the convex hull of the left half points and the right half points, then the problem now is to merge these two convex hulls and determine the convex hull for the complete set. This can be done by finding the upper and lower tangent to the right and left convex hulls. This is illustrated here Tangents between two convex polygons Let the left convex hull be a and the right convex hull be b. Then the lower and upper tangents are named as 1 and 2 respectively, as shown in the figure. Then the red outline shows the final convex hull.
Now the problem remains, how to find the convex hull for the left and right half. Now recursion comes into the picture, we divide the set of points until the number of points in the set is very small, say 5, and we can find the convex hull for these points by the brute algorithm. The merging of these halves would result in the convex hull for the complete set of points. Note: We have used the brute algorithm to find the convex hull for a small number of points and it has a time complexity of  . But some people suggest the following, the convex hull for 3 or fewer points is the complete set of points. This is correct but the problem comes when we try to merge a left convex hull of 2 points and right convex hull of 3 points, then the program gets trapped in an infinite loop in some special cases. So, to get rid of this problem I directly found the convex hull for 5 or fewer points by
. But some people suggest the following, the convex hull for 3 or fewer points is the complete set of points. This is correct but the problem comes when we try to merge a left convex hull of 2 points and right convex hull of 3 points, then the program gets trapped in an infinite loop in some special cases. So, to get rid of this problem I directly found the convex hull for 5 or fewer points by  algorithm, which is somewhat greater but does not affect the overall complexity of the algorithm.
algorithm, which is somewhat greater but does not affect the overall complexity of the algorithm.
Below are the implementation:
CPP
// A divide and conquer program to find convex
// hull of a given set of points.
#include<bits/stdc++.h>
using namespace std;
// stores the centre of polygon (It is made
// global because it is used in compare function)
pair<int, int> mid;
// determines the quadrant of a point
// (used in compare())
int quad(pair<int, int> p)
{
if (p.first >= 0 && p.second >= 0)
return 1;
if (p.first <= 0 && p.second >= 0)
return 2;
if (p.first <= 0 && p.second <= 0)
return 3;
return 4;
}
// Checks whether the line is crossing the polygon
int orientation(pair<int, int> a, pair<int, int> b,
pair<int, int> c)
{
int res = (b.second-a.second)*(c.first-b.first) -
(c.second-b.second)*(b.first-a.first);
if (res == 0)
return 0;
if (res > 0)
return 1;
return -1;
}
// compare function for sorting
bool compare(pair<int, int> p1, pair<int, int> q1)
{
pair<int, int> p = make_pair(p1.first - mid.first,
p1.second - mid.second);
pair<int, int> q = make_pair(q1.first - mid.first,
q1.second - mid.second);
int one = quad(p);
int two = quad(q);
if (one != two)
return (one < two);
return (p.second*q.first < q.second*p.first);
}
// Finds upper tangent of two polygons 'a' and 'b'
// represented as two vectors.
vector<pair<int, int>> merger(vector<pair<int, int> > a,
vector<pair<int, int> > b)
{
// n1 -> number of points in polygon a
// n2 -> number of points in polygon b
int n1 = a.size(), n2 = b.size();
int ia = 0, ib = 0;
for (int i=1; i<n1; i++)
if (a[i].first > a[ia].first)
ia = i;
// ib -> leftmost point of b
for (int i=1; i<n2; i++)
if (b[i].first < b[ib].first)
ib=i;
// finding the upper tangent
int inda = ia, indb = ib;
bool done = 0;
while (!done)
{
done = 1;
while (orientation(b[indb], a[inda], a[(inda+1)%n1]) >=0)
inda = (inda + 1) % n1;
while (orientation(a[inda], b[indb], b[(n2+indb-1)%n2]) <=0)
{
indb = (n2+indb-1)%n2;
done = 0;
}
}
int uppera = inda, upperb = indb;
inda = ia, indb=ib;
done = 0;
int g = 0;
while (!done)//finding the lower tangent
{
done = 1;
while (orientation(a[inda], b[indb], b[(indb+1)%n2])>=0)
indb=(indb+1)%n2;
while (orientation(b[indb], a[inda], a[(n1+inda-1)%n1])<=0)
{
inda=(n1+inda-1)%n1;
done=0;
}
}
int lowera = inda, lowerb = indb;
vector<pair<int, int>> ret;
//ret contains the convex hull after merging the two convex hulls
//with the points sorted in anti-clockwise order
int ind = uppera;
ret.push_back(a[uppera]);
while (ind != lowera)
{
ind = (ind+1)%n1;
ret.push_back(a[ind]);
}
ind = lowerb;
ret.push_back(b[lowerb]);
while (ind != upperb)
{
ind = (ind+1)%n2;
ret.push_back(b[ind]);
}
return ret;
}
// Brute force algorithm to find convex hull for a set
// of less than 6 points
vector<pair<int, int>> bruteHull(vector<pair<int, int>> a)
{
// Take any pair of points from the set and check
// whether it is the edge of the convex hull or not.
// if all the remaining points are on the same side
// of the line then the line is the edge of convex
// hull otherwise not
set<pair<int, int> >s;
for (int i=0; i<a.size(); i++)
{
for (int j=i+1; j<a.size(); j++)
{
int x1 = a[i].first, x2 = a[j].first;
int y1 = a[i].second, y2 = a[j].second;
int a1 = y1-y2;
int b1 = x2-x1;
int c1 = x1*y2-y1*x2;
int pos = 0, neg = 0;
for (int k=0; k<a.size(); k++)
{
if (a1*a[k].first+b1*a[k].second+c1 <= 0)
neg++;
if (a1*a[k].first+b1*a[k].second+c1 >= 0)
pos++;
}
if (pos == a.size() || neg == a.size())
{
s.insert(a[i]);
s.insert(a[j]);
}
}
}
vector<pair<int, int>>ret;
for (auto e:s)
ret.push_back(e);
// Sorting the points in the anti-clockwise order
mid = {0, 0};
int n = ret.size();
for (int i=0; i<n; i++)
{
mid.first += ret[i].first;
mid.second += ret[i].second;
ret[i].first *= n;
ret[i].second *= n;
}
sort(ret.begin(), ret.end(), compare);
for (int i=0; i<n; i++)
ret[i] = make_pair(ret[i].first/n, ret[i].second/n);
return ret;
}
// Returns the convex hull for the given set of points
vector<pair<int, int>> divide(vector<pair<int, int>> a)
{
// If the number of points is less than 6 then the
// function uses the brute algorithm to find the
// convex hull
if (a.size() <= 5)
return bruteHull(a);
// left contains the left half points
// right contains the right half points
vector<pair<int, int>>left, right;
for (int i=0; i<a.size()/2; i++)
left.push_back(a[i]);
for (int i=a.size()/2; i<a.size(); i++)
right.push_back(a[i]);
// convex hull for the left and right sets
vector<pair<int, int>>left_hull = divide(left);
vector<pair<int, int>>right_hull = divide(right);
// merging the convex hulls
return merger(left_hull, right_hull);
}
// Driver code
int main()
{
vector<pair<int, int> > a;
a.push_back(make_pair(0, 0));
a.push_back(make_pair(1, -4));
a.push_back(make_pair(-1, -5));
a.push_back(make_pair(-5, -3));
a.push_back(make_pair(-3, -1));
a.push_back(make_pair(-1, -3));
a.push_back(make_pair(-2, -2));
a.push_back(make_pair(-1, -1));
a.push_back(make_pair(-2, -1));
a.push_back(make_pair(-1, 1));
int n = a.size();
// sorting the set of points according
// to the x-coordinate
sort(a.begin(), a.end());
vector<pair<int, int> >ans = divide(a);
cout << "convex hull:\n";
for (auto e:ans)
cout << e.first << " "
<< e.second << endl;
return 0;
}
Java
// A divide and conquer program to find convex
// hull of a given set of points.
import java.util.*;
public class ConvexHullDivideConquer {
// Method to find the convex hull using the Divide and
// Conquer Algorithm
public static List<int[]> convexHull(int[][] points)
{
if (points.length < 3) {
return Arrays.asList(points);
}
Arrays.sort(points,
(a, b)
-> a[0] != b[0] ? a[0] - b[0]
: a[1] - b[1]);
List<int[]> upper = new ArrayList<>();
List<int[]> lower = new ArrayList<>();
for (int[] point : points) {
while (upper.size() >= 2
&& isNotRightTurn(
upper.get(upper.size() - 2),
upper.get(upper.size() - 1),
point)) {
upper.remove(upper.size() - 1);
}
upper.add(point);
}
for (int i = points.length - 1; i >= 0; i--) {
int[] point = points[i];
while (lower.size() >= 2
&& isNotRightTurn(
lower.get(lower.size() - 2),
lower.get(lower.size() - 1),
point)) {
lower.remove(lower.size() - 1);
}
lower.add(point);
}
HashSet<int[]> hull = new HashSet<>(upper);
hull.addAll(lower);
return new ArrayList<>(hull);
}
// to check correct direction
private static boolean isNotRightTurn(int[] a, int[] b,
int[] c)
{
return (b[0] - a[0]) * (c[1] - a[1])
- (b[1] - a[1]) * (c[0] - a[0])
<= 0;
}
// Main method to test the implementation
public static void main(String[] args)
{
int[][] points
= { { 0, 0 }, { 1, -4 }, { -1, -5 },
{ -5, -3 }, { -3, -1 }, { -1, -3 },
{ -2, -2 }, { -1, -1 }, { -2, -1 },
{ -1, 1 } };
List<int[]> hull = convexHull(points);
System.out.println("Convex Hull:");
for (int[] point : hull) {
System.out.println(point[0] + " " + point[1]);
}
}
}
// This code is contributed by NarasingaNikhil
C#
using System;
using System.Collections.Generic;
namespace ConvexHullDivideAndConquer
{
class Program
{
static void Main(string[] args)
{
Point[] points = new Point[] {
new Point(0, 0),
new Point(1, -4),
new Point(-1, -5),
new Point(-5, -3),
new Point(-3, -1),
new Point(-1, -3),
new Point(-2, -2),
new Point(-1, -1),
new Point(-2, -1),
new Point(-1, 1)
};
List<Point> hull = ComputeConvexHull(points);
Console.WriteLine("Convex Hull:");
foreach (Point p in hull)
{
Console.WriteLine(p.X + " " + p.Y);
}
}
static List<Point> ComputeConvexHull(Point[] points)
{
List<Point> hull = new List<Point>();
// Sort points by x-coordinate
Array.Sort(points);
// Compute upper hull
for (int i = 0; i < points.Length; i++)
{
while (hull.Count >= 2 && Point.CrossProduct(
hull[hull.Count - 2], hull[hull.Count - 1], points[i]) <= 0)
{
hull.RemoveAt(hull.Count - 1);
}
hull.Add(points[i]);
}
// Compute lower hull
int lowerHullIndex = hull.Count + 1;
for (int i = points.Length - 2; i >= 0; i--)
{
while (hull.Count >= lowerHullIndex && Point.CrossProduct(
hull[hull.Count - 2], hull[hull.Count - 1], points[i]) <= 0)
{
hull.RemoveAt(hull.Count - 1);
}
hull.Add(points[i]);
}
// Remove last point (it's a duplicate of the first point)
hull.RemoveAt(hull.Count - 1);
return hull;
}
}
class Point : IComparable<Point>
{
public int X { get; }
public int Y { get; }
public Point(int x, int y)
{
X = x;
Y = y;
}
public int CompareTo(Point other)
{
if (X != other.X)
{
return X - other.X;
}
return Y - other.Y;
}
public static int CrossProduct(Point A, Point B, Point C)
{
return (B.X - A.X) * (C.Y - A.Y) - (B.Y - A.Y) * (C.X - A.X);
}
}
}
Javascript
// Nikunj Sonigara
// Method to find the convex hull using the Divide and Conquer Algorithm
function convexHull(points) {
if (points.length < 3) {
return points;
}
points.sort((a, b) => a[0] !== b[0] ? a[0] - b[0] : a[1] - b[1]);
const upper = [];
const lower = [];
for (const point of points) {
while (upper.length >= 2 && isNotRightTurn(upper[upper.length - 2],
upper[upper.length - 1], point)) {
upper.pop();
}
upper.push(point);
}
for (let i = points.length - 1; i >= 0; i--) {
const point = points[i];
while (lower.length >= 2 && isNotRightTurn(lower[lower.length - 2],
lower[lower.length - 1], point)) {
lower.pop();
}
lower.push(point);
}
const hull = new Set([...upper, ...lower]);
return Array.from(hull);
}
// Nikunj Sonigara
// Function to check the correct direction
function isNotRightTurn(a, b, c) {
return (b[0] - a[0]) * (c[1] - a[1]) - (b[1] - a[1]) * (c[0] - a[0]) <= 0;
}
// Main method to test the implementation
function main() {
const points = [
[0, 0],
[1, -4],
[-1, -5],
[-5, -3],
[-3, -1],
[-1, -3],
[-2, -2],
[-1, -1],
[-2, -1],
[-1, 1]
];
const hull = convexHull(points);
console.log("Convex Hull:");
for (const point of hull) {
console.log(point[0] + " " + point[1]);
}
}
main();
// Nikunj Sonigara
Python3
# A divide and conquer program to find convex
# hull of a given set of points.
from functools import cmp_to_key
# stores the centre of polygon (It is made
# global because it is used in the bcompare function)
mid = [0, 0]
# determines the quadrant of the point
# (used in compare())
def quad(p):
if p[0] >= 0 and p[1] >= 0:
return 1
if p[0] <= 0 and p[1] >= 0:
return 2
if p[0] <= 0 and p[1] <= 0:
return 3
return 4
# Checks whether the line is crossing the polygon
def orientation(a, b, c):
res = (b[1]-a[1]) * (c[0]-b[0]) - (c[1]-b[1]) * (b[0]-a[0])
if res == 0:
return 0
if res > 0:
return 1
return -1
# compare function for sorting
def compare(p1, q1):
p = [p1[0]-mid[0], p1[1]-mid[1]]
q = [q1[0]-mid[0], q1[1]-mid[1]]
one = quad(p)
two = quad(q)
if one != two:
if one < two:
return -1
return 1
if p[1]*q[0] < q[1]*p[0]:
return -1
return 1
# Finds upper tangent of two polygons 'a' and 'b'
# represented as two vectors.
def merger(a, b):
# n1 -> number of points in polygon a
# n2 -> number of points in polygon b
n1, n2 = len(a), len(b)
ia, ib = 0, 0
# ia -> rightmost point of a
for i in range(1, n1):
if a[i][0] > a[ia][0]:
ia = i
# ib -> leftmost point of b
for i in range(1, n2):
if b[i][0] < b[ib][0]:
ib = i
# finding the upper tangent
inda, indb = ia, ib
done = 0
while not done:
done = 1
while orientation(b[indb], a[inda], a[(inda+1) % n1]) >= 0:
inda = (inda + 1) % n1
while orientation(a[inda], b[indb], b[(n2+indb-1) % n2]) <= 0:
indb = (indb - 1) % n2
done = 0
uppera, upperb = inda, indb
inda, indb = ia, ib
done = 0
g = 0
while not done: # finding the lower tangent
done = 1
while orientation(a[inda], b[indb], b[(indb+1) % n2]) >= 0:
indb = (indb + 1) % n2
while orientation(b[indb], a[inda], a[(n1+inda-1) % n1]) <= 0:
inda = (inda - 1) % n1
done = 0
ret = []
lowera, lowerb = inda, indb
# ret contains the convex hull after merging the two convex hulls
# with the points sorted in anti-clockwise order
ind = uppera
ret.append(a[uppera])
while ind != lowera:
ind = (ind+1) % n1
ret.append(a[ind])
ind = lowerb
ret.append(b[lowerb])
while ind != upperb:
ind = (ind+1) % n2
ret.append(b[ind])
return ret
# Brute force algorithm to find convex hull for a set
# of less than 6 points
def bruteHull(a):
# Take any pair of points from the set and check
# whether it is the edge of the convex hull or not.
# if all the remaining points are on the same side
# of the line then the line is the edge of convex
# hull otherwise not
global mid
s = set()
for i in range(len(a)):
for j in range(i+1, len(a)):
x1, x2 = a[i][0], a[j][0]
y1, y2 = a[i][1], a[j][1]
a1, b1, c1 = y1-y2, x2-x1, x1*y2-y1*x2
pos, neg = 0, 0
for k in range(len(a)):
if (k == i) or (k == j) or (a1*a[k][0]+b1*a[k][1]+c1 <= 0):
neg += 1
if (k == i) or (k == j) or (a1*a[k][0]+b1*a[k][1]+c1 >= 0):
pos += 1
if pos == len(a) or neg == len(a):
s.add(tuple(a[i]))
s.add(tuple(a[j]))
ret = []
for x in s:
ret.append(list(x))
# Sorting the points in the anti-clockwise order
mid = [0, 0]
n = len(ret)
for i in range(n):
mid[0] += ret[i][0]
mid[1] += ret[i][1]
ret[i][0] *= n
ret[i][1] *= n
ret = sorted(ret, key=cmp_to_key(compare))
for i in range(n):
ret[i] = [ret[i][0]/n, ret[i][1]/n]
return ret
# Returns the convex hull for the given set of points
def divide(a):
# If the number of points is less than 6 then the
# function uses the brute algorithm to find the
# convex hull
if len(a) <= 5:
return bruteHull(a)
# left contains the left half points
# right contains the right half points
left, right = [], []
start = int(len(a)/2)
for i in range(start):
left.append(a[i])
for i in range(start, len(a)):
right.append(a[i])
# convex hull for the left and right sets
left_hull = divide(left)
right_hull = divide(right)
# merging the convex hulls
return merger(left_hull, right_hull)
# Driver Code
if __name__ == '__main__':
a = []
a.append([0, 0])
a.append([1, -4])
a.append([-1, -5])
a.append([-5, -3])
a.append([-3, -1])
a.append([-1, -3])
a.append([-2, -2])
a.append([-1, -1])
a.append([-2, -1])
a.append([-1, 1])
n = len(a)
# sorting the set of the points according
# to x-coordinate
a.sort()
ans = divide(a)
print('Convex Hull:')
for x in ans:
print(int(x[0]), int(x[1]))