Calculate the area of the trapezium if the length of parallel sides is 40 cm and 20 cm and non-parallel sides are equal having the lengths of 26 cm.

Mensuration deals with the quantities pertaining to various geometrical shapes and their measurement. It can be classified into two types: mensuration 2D and mensuration 3D. As the names suggest, the former deals with those shapes which have only two dimensions: length and breadth; while the latter deals with those shapes which have three dimensions: length, breadth, and height. 

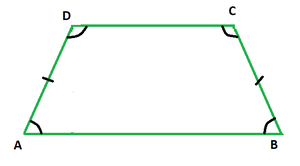
Isosceles Trapezium

An isosceles trapezium is a quadrilateral that has exactly one pair of parallel sides and the other pair is non-parallel and equal in length. Like any other quadrilateral, the sum of its angles always measures 360°. The figure below depicts an isosceles trapezium ABCD, where AB ∥ CD and the non-parallel sides are equal in length, i.e., AD = BC. 

Area of a Trapezium

The area of a trapezium is half the product of the sum of its parallel sides and the distance between the said parallel sides, i.e., the height or altitude of the trapezium.

A = ½ × (a + b) × h

where,

a and b depict the lengths of parallel sides and h is the height of the trapezium.

Calculate the area of the trapezium if the length of parallel sides is 40 cm and 20 cm and non-parallel sides are equal having the lengths of 26 cm.

Solution:

Area of a trapezium = ½ × (a + b) × h  …(i)

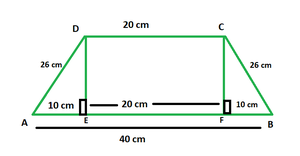
In the figure above, DCEF is a rectangle with l = 20 cm. △ADE and △CFB are both right triangles with hypotenuse 26 cm and base 10 cm each. 

In right △ADE, using Pythagoras Theorem, we have:

AD² = AE² + DE²

⇒ 26² − 10² = DE²

⇒ DE = 24 cm

Thus, height of trapezium = h = 24 cm, a = 20 cm and b = 40 cm.

Substituting the above values in eq. (i), we have:

A = ½ × (20 + 40) × 24

Area of the trapezium = 720 sq. cm.

Similar Problems

Question 1. In a trapezium, the parallel sides measure 20 cm and 10 cm. Calculate the area of the trapezium if its non-parallel sides are equal having lengths of 13 cm.

Solution:

Area of a trapezium = ½ × (a + b) × h  …(i)

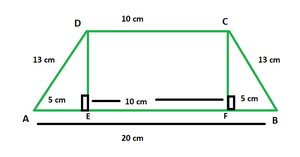
In the figure above, DCEF is a rectangle with l = 10 cm. △ADE and △CFB are both right triangles with hypotenuse 13 cm and base 5 cm each.

In right △ADE, using Pythagoras Theorem, we have:

AD² = AE² + DE²

⇒ 13² − 5² = DE²

⇒ DE = 12 cm

Thus, height of trapezium = h = 12 cm, a = 10 cm and b = 20 cm.

Substituting the above values in eq. (i), we have:

A = ½ × (10 + 20) × 12

Area of the trapezium = 180 sq. cm.

Question 2. In a trapezium, the parallel sides measure 13 cm and 25 cm. Calculate the area of the trapezium if its non-parallel sides are equal having lengths of 10 cm.

Solution:

Area of a trapezium = ½ × (a + b) × h  …(i)

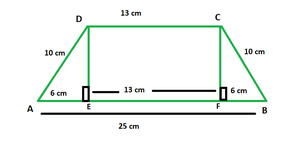
In the figure above, DCEF is a rectangle with l = 13 cm. △ADE and △CFB are both right triangles with hypotenuse 10 cm and base 6 cm each.

In right △ADE, using Pythagoras Theorem, we have:

AD2 = AE² + DE²

⇒ 10² − 6² = DE²

⇒ DE = 8 cm

Thus, height of trapezium = h = 8 cm, a = 13 cm and b = 25 cm.

Substituting the above values in eq. (i), we have:

A = ½ × (13 + 25) × 8

Area of the trapezium = 152 sq. cm.

Question 3. In a trapezium, the parallel sides measure 40 cm and 70 cm. Calculate the area of the trapezium if its non-parallel sides are equal having lengths of 25 cm.

Solution:

Area of a trapezium = ½ × (a + b) × h  …(i)

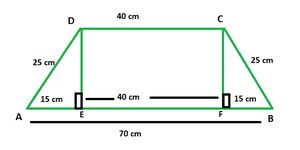
In the figure above, DCEF is a rectangle with l = 40 cm. △ADE and △CFB are both right triangles with hypotenuse 25 cm and base 15 cm each.

In right △ADE, using Pythagoras Theorem, we have:

AD² = AE² + DE²

⇒ 25² − 15² = DE²

⇒ DE = 20 cm

Thus, height of trapezium = h = 20 cm, a = 40 cm and b = 70 cm.

Substituting the above values in eq. (i), we have:

A = ½ × (40 + 70) × 20

Area of the trapezium = 1100 sq. cm.

Question 4. In a trapezium, the parallel sides measure 40 cm and 10 cm. Calculate the area of the trapezium if its non-parallel sides are equal having lengths of 25 cm.

Solution:

Area of a trapezium = ½ × (a + b) × h  …(i)

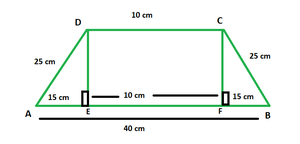
In the figure above, DCEF is a rectangle with l = 13 cm. △ADE and △CFB are both right triangles with hypotenuse 10 cm and base 6 cm each.

In right △ADE, using Pythagoras Theorem, we have:

AD² = AE² + DE²

⇒ 25² − 15² = DE²

⇒ DE = 20 cm

Thus, height of trapezium = h = 20 cm, a = 10 cm and b = 40 cm.

Substituting the above values in eq. (i), we have:

A = ½ × (10 + 40) × 20

Area of the trapezium = 500 sq. cm.

My Personal Notes arrow_drop_up

Save