We hear sound whenever we talk, listen to some music, or play any musical instrument, etc. But did you ever wondered what is that sound and how is it produced? Or why do we hear to our own voice when we shout in a big empty room loudly? What are the ranges of sound that we can hear? In this article, we will find answers to all these questions.
What is Sound?
A sound is a vibration propagating or travelling through any medium in the form of a mechanical wave. The medium in which the waves propagate or travel can either be a solid medium, a liquid, or a gas medium. Sound travels the fastest in solid medium, relatively slower than solid in liquids, and slowest among the three in gases. In other words, any vibration that propagates as an audible or hear-able wave of a pressure, through a medium such as a gas, liquid, or solid.
It is also defined as the reception of the sound pressure waves and their perception or observation and interpretation by the brain.
A sound wave is also the pattern of the disturbances caused by the energy traveling away from the source of the sound. Sound waves are referred also as longitudinal waves. Meaning the propagation of vibration of particles is somewhat parallel to the direction of the energy wave propagation. These high-pressure and also low-pressure regions are termed compressions and the rarefactions, respectively.
Different Factors Affecting Sound Characteristics
The sound waves produced by a guitar is different from the sound that is produced by a drum. The reason being the sound waves produced by different sources have different characteristics. Sound can also be characterized by its frequency, wavelength, and amplitude.
Frequency of sound
The number of rarefactions of the sound waves and the compressions occurring per unit of time is known as the frequency of a sound wave. The formula of the frequency is given as:
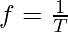
- f = frequency of a sound wave
- T = time period.
Wavelength of sound
The distance between the successive compression and also the rarefaction of sound waves known as the wavelength of a sound wave. The wavelength formula is given as follows:
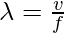
Where,
- f = frequency of the sound wave
- v = velocity of the sound wave.
Amplitude of sound
The amplitude of the sound is referred to as the magnitude of the maximum disturbance in a sound wave. The amplitude is also referred to as a measure of energy. Higher is the amplitude so higher is the energy in a sound wave. Humans can only hear a limited range of frequencies of the sound wave. Physicists found the audio frequency spectrum of the human ear lies between 20 Hz and 20,000 Hz.
Speed of Sound
The speed or velocity at which the sound waves propagate or travel through a medium is known as the speed of sound. The speed of sound is different for different media. The speed of sound is greatest in solids because the atoms in solid are highly compressed whereas least in gases for the same reason of molecular compression which is least in it. The formula derived for the speed of a sound wave is:
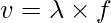
Where,
v = velocity of sound wave
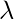 = wavelength of sound wave
= wavelength of sound wave
f = frequency of sound wave
The table provided below lists the speed of sound waves in different media.
Medium
| Speed of Sound Waves
|
| Air | 343.2 m/s |
| Water | 1481 m/s |
| Hydrogen | 1270 m/s |
| Copper | 4600 m/s |
| Glass | 4540 m/s |
Types of Sound Based On Frequency of Perception
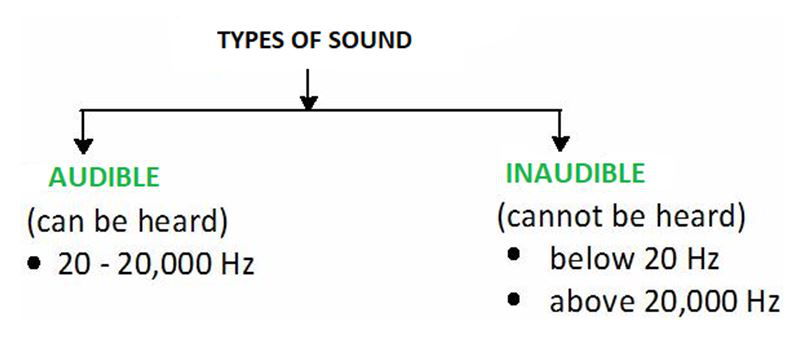
Audible Sound
The human ear can easily detect or sense the frequencies which lie between 20 Hz and 20 kHz. Hence, the sound waves with a frequency ranging from 20 Hz to 20 kHz is known as audible sounds. The human ear is sensitive for every minute pressure difference occurring in the air if they lie in the audible frequency ranges. They can detect the pressure differences that are of less than one billionth of the atmospheric pressure. As we grow and become exposed to any sound for a longer time, our ears get impaired or get damaged and the upper limit of the audible frequencies decreases. For a normal middle-aged person, the highest frequency which he or she can hear is 12-14 kilohertz.
Examples of the vibrating sources that produce or makes the sound which is in the human audible range of frequencies we can hear are of drums, guitar strings, tuning fork.
Human vocal cords singing songs.
Diaphragms of the loudspeakers producing sound or loud music.
The speakers used in restaurants or in events like marriage, birthday parties.
The danger signals also lie in audible range so that we can perceive them.
Inaudible Sound
Human ear cannot detect or perceive sound frequencies which are less than 20 vibrations per second i.e. of 20 Hz. Therefore, any sound wave below this frequency will be inaudible for humans. Also in the high-frequency range, the human ear cannot detect or perceive the frequencies that lie above 20,000 vibrations per second (20 kHz) and the amplitude of the sound wave would be dependent on its loudness. Therefore, the frequencies lying below 20 Hz and above 20 kHz comes under the category of the inaudible frequencies. The low-frequency sounds which the human ear cannot perceive or detect are also known as infrasonic sounds. Also, the higher range inaudible frequency is also known as ultrasonic sound.
Some animals for example the special dogs have the ability to hear sounds that are having frequencies higher than the 20 kHz. The police officers use whistles having frequencies higher than the 20 kHz so that only dogs can perceive or listen to it.
Inaudible frequencies are also helpful for many purposes. These are also used in many fields like in research and also in medicine purposes.
The ultrasound devices or equipment that are used for the tracking and for studying many medical problems work at a frequency above the 20 kHz.
Infrasonic Sound
Infrasonic sound or sometimes referred to as the low-frequency sound waves describes the waves with a frequency below the lower limit of audibility of the human ear (generally it is 20 Hz). Hearing becomes gradually or moreover less sensitive as the frequency decreases, so for the humans to perceive or detect the infrasound, the sound pressure needs to be sufficiently high. Animals that can communicate or talk with one another using infrasonic sounds are; Rhinos, hippos, elephants, octopus, pigeons, squid, cuttlefish, cod, Guinea fowl.
Applications of infrasonic sound waves:
- Elephants and also Giraffes use the infrasonic sound waves to communicate between their herds over a greater distance.
- Scientists are widely using microphones to track the herd of animals even if they are hidden somewhere in dense areas.
- Infrasound waves can be used to detect volcanic eruptions.
- Scientists can use infra-sound to track the meteors through atmosphere.
Ultrasonic Sound
The sounds having a large or too high frequency that cannot be heard or detected by the human ear are called ultrasonic sounds. The sounds of the frequency which are greater than 20,000 hertz are called ultrasonic. The ultrasonic sounds cannot be heard or perceived by human beings. Humans can neither produce the ultrasonic sound waves nor can they hear detect ultrasonic sounds.
These waves are used for the following purposes:
- Ultrasonic waves are used for flaw detection.
- Cutting and the matching of the hard materials.
- Ultrasonic soldering and also welding.
- Measurement of the flow devices.
- Wide applications in medicine.
- Ultrasonic as means of communication at distant places.
Factors Affecting Propagation Of Sound Waves
There are major two factors that affect the speed of the sound:
- Density of the medium: For the sound to travel in the medium, there is a need for any medium and the density of the medium is considered one of the factors on which its speed depends. Whenever the medium is denser, the molecules of the medium are closely packed to each other which means that the sound waves travel faster. Therefore, the speed of sound perceived increases as the density of the medium goes on increasing.
- Another is the temperature of the medium where it propagates: The temperature of the taken medium and the sound waves are directly proportional or dependent on each other. Therefore, as we increase the temperature, the speed of sound also increases proportionally.
Sample Questions
Question 1: An instrument produces a sound of frequency 250 Hz. Will be able to perceive its sound?
Solution:
Yes, we will be able to perceive its sound as it falls under our audible range that is between 20 Hz – 20,000 Hz.
20 Hz < 250 Hz < 20,000 Hz
Question 2: A bagpiper produces a sound of frequency 360 Hz. Can he be able to gather any audience with his music?
Solution:
Yes, he will be able to gather audience as its musical sound falls under the audible range that is between 20 Hz – 20,000 Hz.
20 Hz < 360 Hz < 20,000 Hz
Question 3: A machine produces a sound of frequency 25,000 Hz. Will the people near the manufacturing hub be able to perceive its sound?
Solution:
No, they will not be able to perceive its sound as it doesn’t fall under our audible range that is between 20 Hz – 20,000 Hz.
20 Hz < 20,000 Hz< 25,000 Hz
Question 4: Calculate the frequency of waves if the time period given is 25 sec.
Solution:
As we know,
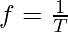
Where f=? And T= 25 sec
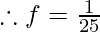
f= 0.04 Hz.
Therefore, the frequency is 0.04 Hz.
Question 5: Calculate the frequency of waves if the time period given is 50 sec.
Solution:
As we know,
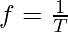
Where f=? And T=50 sec
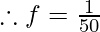
f= 0.02 Hz.
Therefore, the frequency is 0.02 Hz.
Question 6: What is the time period if the frequency of the wave is 2 Hz?
Solution:
As we know,
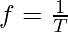
Where f= 2 Hz And T= ?
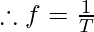
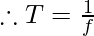
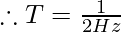
Therefore, the Time period is 0.5 sec.
Question 7: Calculate the frequency if the velocity is 3 m/s and the wavelength is 30m.
Solution:
As we know,
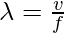
Where, v = 2m/ s and f= 2 Hz

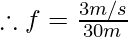
f = 0.1 Hz
The frequency is 0.1 Hz.
Question 8: Calculate the wavelength if the velocity is 2 m/s and the frequency is 2 Hz.
Solution:
As we know,
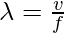
Where, v = 2m/ s and f= 2 Hz
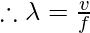
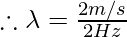
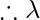 = 1 m.
= 1 m.
The wavelength is 1m.
Question 9: Calculate the velocity if the wavelength is 12 m and the frequency is 12 Hz.
Solution:
As we know,
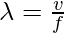
Where, 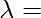 2m and f= 12 Hz
2m and f= 12 Hz
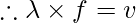
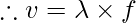
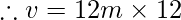 Hz
Hz
The velocity is 144 m/s.
Share your thoughts in the comments
Please Login to comment...