Logic functions and Minimization

Question 1

Consider the Boolean function z(a,b,c). Which one of the following minterm lists represents the circuit given above ?

• z = ∑(0, 1, 3, 7)
• z = ∑(1, 4, 5, 6, 7)
• z = ∑(2, 4, 5, 6, 7)
• z = ∑(2, 3, 5)

Question 2

Let p and q be two propositions. Consider the following two formulae in propositional logic.

S1:  (¬p∧(p∨q))→q
S2:  q→(¬p∧(p∨q)) 

Which one of the following choices is correct?

• Both S1 and S2 are tautologies.
• S1 is a tautology but S2 is not a tautology
• S1 is not a tautology but S2 is a tautology
• Neither S1 nor S2 is a tautology

Question 3

Consider the following Boolean expression.

F=(X+Y+Z)(X\'+Y)(Y\'+Z) 

Which of the following Boolean expressions is/are equivalent to F\' (complement of F)?

• (X\'+Y\'+Z\')(X+Y\')(Y+Z\')
• XY\'+Z\'
• (X+Z\')(Y\'+Z\')
• XY\'+YZ\'+X\'Y\'Z\'

Question 4

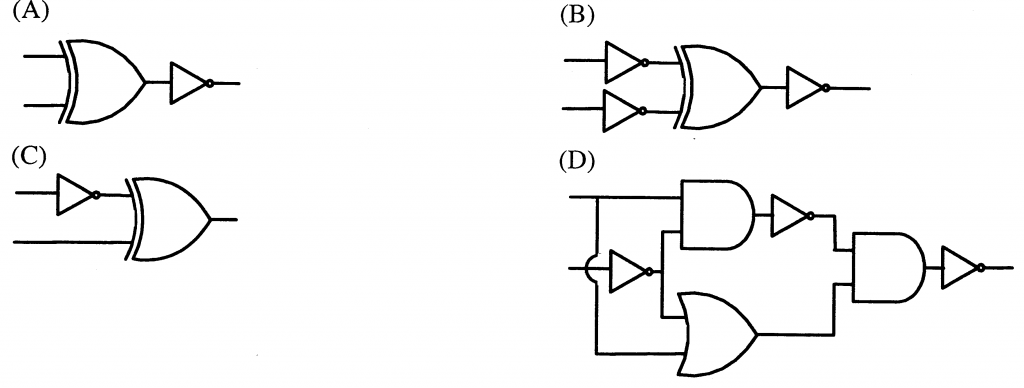
Which one of the following expressions does NOT represent exclusive NOR of x and y?

• xy+x\'y\'
• x⊕y\'
• x\'⊕y
• x\'⊕y\'

Question 5

What is the minimal form of the Karnaugh map shown below? Assume that X denotes a don’t care term.

[caption width="800"] [/caption]

• b\'d\'

• b\'d\' + b\'c\'

• b\'d\' + a\'b\'c\'d\'

• b\'d\' + b\'c\' + c\'d\'

Question 6

Which one of the following circuits is NOT equivalent to a 2-input XNOR (exclusive NOR) gate?

• A
• B
• C
• D

Question 7

The simplified SOP (Sum Of Product) form of the boolean expression (P + Q\' + R\') . (P + Q\' + R) . (P + Q + R\') is

• (P\'.Q + R\')
• (P + Q\'.R\')
• (P\'.Q + R)
• (P.Q + R)

Question 8

The minterm expansion of f(P, Q, R) = PQ + QR\' + PR\' is

• m2 + m4 + m6 + m7
• m0 + m1 + m3 + m5
• m0 + m1 + m6 + m7
• m2 + m3 + m4 + m5

Question 9

What is the minimum number of gates required to implement the Boolean function (AB+C)if we have to use only 2-input NOR gates?

• 2
• 3
• 4
• 5

Question 10

In the Karnaugh map shown below, X denotes a don\'t care term. What is the minimal form of the function represented by the Karnaugh map?

A)   


B) 

C) 

D)  

• A

• B

• C

• D