GATE-CS-2009

Question 1

Which one of the following in NOT necessarily a property of a Group?

• A. Commutativity
• B. Associativity
• C. Existence of inverse for every element
• D. Existence of identity

Answer: (A)

A group is a set, G, together with an operation • (called the group law of G) that combines any two elements a and b to form another element, denoted a • b or ab. To qualify as a group, the set and operation, (G, •), must satisfy four requirements known as the group axioms: Closure For all a, b in G, the result of the operation, a • b, is also in G.b Associativity For all a, b and c in G, (a • b) • c = a • (b • c). Identity element There exists an element e in G, such that for every element a in G, the equation e • a = a • e = a holds. Such an element is unique (see below), and thus one speaks of the identity element. Inverse element For each a in G, there exists an element b in G such that a • b = b • a = e, where e is the identity element. The result of an operation may depend on the order of the operands. In other words, the result of combining element a with element b need not yield the same result as combining element b with element a; the equation a • b = b • a may not always be true. This equation always holds in the group of integers under addition, because a + b = b + a for any two integers (commutativity of addition). Groups for which the commutativity equation a • b = b • a always holds are called abelian groups (in honor of Niels Abel) Source: http://en.wikipedia.org/wiki/Group_(mathematics)

Question 2

What is the chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle? Assume n >= 2.

• A. n-1
  
• B. 3
  
• C. 2
  
• D. n
  

Answer: (C)

The chromatic number of a graph is the smallest number of colours needed to colour the vertices of so that no two adjacent vertices share the same colour. These types of questions can be solved by substitution with different values of n. 

1) n = 2 

This simple graph can be coloured with 2 colours. 

2) n = 3 

Here, in this graph let us suppose vertex A is coloured with C1 and vertices B, C can be coloured with colour C2 => chromatic number is 2 In the same way, you can check with other values, Chromatic number is equals to 2 

A simple graph with no odd cycles is bipartite graph and a Bipartite graph can be colored using 2 colors

Question 3

Which one of the following is TRUE for any simple connected undirected graph with more than 2 vertices?

• A. No two vertices have the same degree.
• B. At least two vertices have the same degree.
• C. At least three vertices have the same degree.
• D. All vertices have the same degree.

Answer: (B)

Since the graph is simple, there must not be any self loop and parallel edges. Since the graph is connected, the degree of any vertex cannot be 0. Therefore, degree of all vertices should be from 1 to n-1. So the degree of at least two vertices must be same.

Question 4

Consider the binary relation R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?

• A. R is symmetric but NOT antisymmetric
• B. R is NOT symmetric but antisymmetric
• C. R is both symmetric and antisymmetric
• D. R is neither symmetric nor antisymmetric

Answer: (D)

R is not symmetric as (x, y) is present, but (y, x) is not present in R. R is also not antisymmetric as both (x, z) and (z, x) are present in R.

Question 5

(1217)₈ is equivalent to

• A. (1217)₁₆
• B. (028F)₁₆
• C. (2297)₁₀
• D. (0B17)₁₆

Answer: (B)

(1217)₈ = (001 010 001 111)₈ = (0010 1000 1111) = (28F)₁₆

Question 6

What is the minimum number of gates required to implement the Boolean function (AB+C)if we have to use only 2-input NOR gates?

• A. 2
• B. 3
• C. 4
• D. 5

Answer: (B)

AB+C = (A+C)(B+C) = ((A+C)' + (B+C)')' So, '3' 2-input NOR gates are required.

Question 7

A CPU generally handles an interrupt by executing an interrupt service routine

• A. As soon as an interrupt is raised
• B. By checking the interrupt register at the end of fetch cycle.
• C. By checking the interrupt register after finishing the execution of the current instruction.
• D. By checking the interrupt register at fixed time intervals.

Answer: (C)

Hardware detects interrupt immediately, but CPU acts only after its current instruction. This is followed to ensure integrity of instructions.

Question 8

In which one of the following page replacement policies, Belady’s anomaly may occur?

• A. FIFO
• B. Optimal
• C. LRU
• D. MRU

Answer: (A)

Belady’s anomaly proves that it is possible to have more page faults when increasing the number of page frames while using the First in First Out (FIFO) page replacement algorithm. See the wiki page for an example of increasing page faults with number of page frames.

Question 9

The essential content(s) in each entry of a page table is / are

• A. Virtual page number
• B. Page frame number
• C. Both virtual page number and page frame number
• D. Access right information

Answer: (B)

A page table entry must contain Page frame number. Virtual page number is typically used as index in page table to get the corresponding page frame number. See this for details.

Question 10

What is the number of swaps required to sort n elements using selection sort, in the worst case? (A) 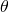(n) (B) 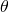(n log n) (C) 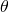(n^2 ) (D) 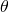(n^2 log n)

• A. Theta(n)
• B. Theta(nLogn)
• C. Theta(n*n)
• D. Theta(n*nLogn)

Answer: (A)

Here is Selection Sort algorithm for sorting in ascending order.

   1. Find the minimum value in the list
   2. Swap it with the value in the first position
   3. Repeat the steps above for the remainder of the list (starting at
      the second position and advancing each time)

As we can see from the algorithm, selection sort performs swap only after finding the appropriate position of the current picked element. So there are O(n) swaps performed in selection sort. Because swaps require writing to the array, selection sort is preferable if writing to memory is significantly more expensive than reading. This is generally the case if the items are huge but the keys are small. Another example where writing times are crucial is an array stored in EEPROM or Flash. There is no other algorithm with less data movement. References: http://en.wikipedia.org/wiki/Selection_sort