Gate IT 2005

Question 1

A bag contains 10 blue marbles, 20 green marbles and 30 red marbles. A marble is drawn from the bag, its colour recorded and it is put back in the bag. This process is repeated 3 times. The probability that no two of the marbles drawn have the same colour is

• A. 1/36
• B. 1/6
• C. 1/4
• D. 1/3

Answer: (B)

As number of colors is 3,Possible combinations -> 3! = 6 Probability of Blue  marble: 10/60 Probability of Green  marble: 20/60 Probability of Red marble: 30/60 Probability that no two of the marbles drawn have the same colour is = 6 * (10/60 * 20/60 * 30/60) = 1/6 Therefore B is the Answer

Question 2

If the trapezoidal method is used to evaluate the integral obtained ₀∫¹x²dx ,then the value obtained

• A. is always > (1/3)
• B. is always < (1/3)
• C. is always = (1/3)
• D. may be greater or lesser than (1/3)

Answer: (A)

Question 3

The determinant of the matrix given below is

• A. -1
• B. 0
• C. 1
• D. 2

Answer: (A)

  Matrices don’t have value associated with them, but determinant have value associated with them. Determinant of a matrix can be find out by taking any one row or one column, in this row or column, multiplying each element with its cofactor and summing the value up. This solution is contributed by Sandeep Pandey.

Question 4

Let L be a regular language and M be a context-free language, both over the alphabet Σ. Let Lc and Mc denote the complements of L and M respectively. Which of the following statements about the language Lc∪ Mc is TRUE

• A. It is necessarily regular but not necessarily context-free
• B. It is necessarily context-free.
• C. It is necessarily non-regular.
• D. None of the above

Answer: (D)

Proposition: L is a regular language M is a context free language Derivation: L_c  union M_c = complement{L intersection M} Now, L intersection M is a CFL according to closure laws of CFLs, i.e. intersection of a CFL with RL is always a CFL. But, complement{L intersection M} might not be a CFL because complement over CFL doesn't guarantee a CFL. It can even be a RL or it might even lie outside the CFL circle. It will be a context-sensitive language certainly, but nothing else can be said about it. Conclusion: Considering the above derivation, none of the statements are true. Hence correct answer would be (D) None of the above. Related article : http://quiz.geeksforgeeks.org/theory-of-computation-closure-properties-of-context-free-languages/ This solution is contributed by Vineet Purswani.

Question 5

Which of the following statements is TRUE about the regular expression 01*0?

• A. It represents a finite set of finite strings.
• B. It represents an infinite set of finite strings.
• C. It represents a finite set of infinite strings.
• D. It represents an infinite set of infinite strings

Answer: (B)

First of all, A string can never be infinite because String is a finite sequence of symbols over Σ So option (c) and (d) are eliminated. And because of star(*) it can generate infinite set. So Option (B) is CORRECT.   This solution is contributed by Abhishek Agrawal.

Question 6

The language {0ⁿ 1ⁿ 2ⁿ | 1 ≤ n ≤ 10⁶} is  

• A. regular
• B. context-free but not regular.
• C. context-free but its complement is not context-free.
• D. not context-free

Answer: (A)

The value of ‘n’ is finite. So, only finite number of strings can be part of given language. Therefore, we can construct a finite state automata for this language.

Thus, option (A) is correct.

Please comment below if you find anything wrong in the above post.

Question 7

Which of the following expressions is equivalent to (A⊕B)⊕C

• A. (A+B+C)(A¯+B¯+C¯)
• B. (A+B+C)(A¯+B¯+C)
• C. ABC+A¯(B⊕C)+B¯(A⊕C)
• D. None

Answer: (C)

(A ⊕ B) ⊕ C

By Solving, We get
= (A ⊕ B)′ C + (A ⊕ B) C′

The above expression can be written as:
= (A ⊙ B) C + (A ⊕ B) C′

Now,

= (AB + A′B′) C + (A ⊕ B) C′

= ABC + A′B′C + AB′C′ + A′BC′	     [As: X + X = X]				     
			         [So, A′B′C + A′B′C = A′B′C]
= ABC + (A′B′C + A′B′C) + AB′C′ + A′BC′

This can be written as:

= ABC + A′ (B ⊕ C) + B′ (A ⊕ C)

This explanation has been provided by Saksham Seth.

Question 8

Using Booth's Algorithm for multiplication, the multiplier -57 will be recoded as

• A. 0 -1 0 0 1 0 0 -1
• B. 1 1 0 0 0 1 1 1
• C. 0 -1 0 0 1 0 0 0
• D. 0 1 0 0 -1 0 0 1

Answer: (A)

Booth's algorithm: first take 2's complement of given number if number is negative, then append 0 into LSB.

Then, for each pair from LSB to MSB (add 1 bit at a time):
00 = 0, 01 = +1, 10 = -1, 11 = 0

Therefore, given number in signed representation (2's complementation) of -57

= 2's complement of (00111001) = 11000110+1 = 11000111
= append 0 into LSB of (11000111) = 110001110
Now Booth's code (add 1 bit at a time, from LSB to MSB):
= 11, 10, 00, 00, 01, 11, 11, 10 = 0 -1 0 0 1 0 0 -1

Alternative way - You can calculated decimal values in given options: (A) 0 -1 0 0 1 0 0 -1 = 0*(2^6) -1*(2^6) + 0*(2^5) + 0*(2^4) + 1*(2^3) + 0*(2^2) + 0*(2^1) -1*(2^0) = -2^6 + 2^3 - 2^0 = -64 +8 -1 = -57 (B) 1 1 0 0 0 1 1 1 = 2^7 + 2^6 + 2^2 2^1 + 2^0 = 199 (C) 0 -1 0 0 1 0 0 0 = -2^6 + 2^3 = -56 (D) 0 1 0 0 -1 0 0 1 = 2^6 - 2^3 + 2^0 = 57 So, option (A) is correct.

Question 9

A dynamic RAM has a memory cycle time of 64 nsec. It has to be refreshed 100 times per msec and each refresh takes 100 nsec. What percentage of the memory cycle time is used for refreshing?

• A. 10
• B. 6.4
• C. 1
• D. .64

Answer: (C)

Memory cycle time = 64 ns Memory is refreshed 100 times per msec.
Number of refreshes in 1 memory cycle (i.e in 64 ns) = (100 * 64 * 10^-9) / 10^-3 = 64 * 10^-4.
Time taken for each refresh = 100 ns Time taken for 64 * 10^-4 refreshes = 64 * 10^-4 * 100 * 10^-9 sec = 64 * 10^-11 sec.
Percentage of the memory cycle time used for refreshing : = (Time taken to refresh in 1 memory cycle / Total time) * 100 = (64 * 10^-11 / 64 * 10^-9) * 100 = 1 %

Thus, option (C) is correct.

Please comment below if you find anything wrong in the above post.

Question 10

A two-way switch has three terminals a, b and c. In ON position (logic value 1), a is connected to b, and in OFF position, a is connected to c. Two of these two-way switches S1 and S2 are connected to a bulb as shown below.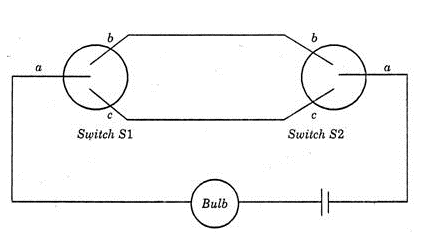 Which of the following expressions, if true, will always result in the lighting of the bulb ?

• A. S1.S2'
• B. S1+S2
• C. (S1⊕S2)'
• D. S1⊕S2

Answer: (C)

If we draw truth table of the above circuit,it'll be S1     S2    Bulb 0         0       On 0         1        Off 1         0        Off 1          1         On = (S1⊕ S2)'   Therefore answer is C