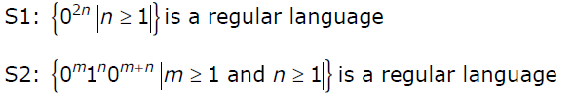GATE-CS-2001
Question 1
Consider the following statements:
S1: The sum of two singular n × n matrices may be non-singular S2: The sum of two n × n non-singular matrices may be singular.Which of the following statements is correct?
Question 2
Consider the following relations:
R1(a,b) if (a+b) is even over the set of integers R2(a,b) if (a+b) is odd over the set of integers R3(a,b) if a.b > 0 over the set of non-zero rational numbers R4(a,b) if |a - b| <= 2 over the set of natural numbers
Which of the following statements is correct?
Question 3
Consider two well-formed formulas in prepositional logic.
F1 : P ⇒ ¬P F2 : ( P⇒¬P)∨(¬P⇒P)
Which of the following statements is correct?
Question 6
Given an arbitary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least
Question 10
Suppose a processor does not have any stack pointer register. Which of the following statements is true?
There are 50 questions to complete.
Last Updated :
Take a part in the ongoing discussion