GATE-CS-2000

Question 1

The minimum number of cards to be dealt from an arbitrarily shuffled deck of 52 cards to guarantee that three cards are from some same suit is

• A. 3
• B. 8
• C. 9
• D. 12

Answer: (C)

Total number of suits is 4 We need minimum 9 cards to make sure that there are 3 cards of same suit. For example, With 8 cards, we can have 2 cards of each suit.

Question 2

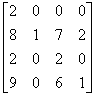
An n x n array v is defined as follows:

v[i, j] = i-j for all i, j, 1 <= i <= n, 1 <= j <= n

The sum of the elements of the array v is

• A. 0
• B. n-1
• C. n² - 3n + 2
• D. n² (n+1)/2

Answer: (A)

In this case, the matrix would be

0    -1    -2    -3    -4    -5    -6    -7    ...    -n
1     0    -1    -2    -3    -4    -5    -6    ...  -(n-1)
2     1     0    -1    -2    -3    -4    -5    ...  -(n-2)
3     2     1     0    -1    -2    -3    -4    ...  -(n-3)
4     3     2     1     0    -1    -2    -3    ...  -(n-4)
5     4     3     2     1     0    -1    -2    ...  -(n-5)
6     5     4     3     2     1     0    -1    ...  -(n-6)
7     6     5     4     3     2     1     0    ...  -(n-6)
.     .     .     .     .     .     .     .     .   .   .
.     .     .     .     .     .     .     .     .   .   .
.     .     .     .     .     .     .     .     .   .   .
n    n-1   n-2   n-3   n-4   n-5   n-6    n-7  ...  2   1

Now, we take the sum of first row and first column, which comes out to be zero. Similarly, we take the sum of second row and second column, third row and third column, and so on, and it is found that all have a sum equal to zero. So, the sum of all the elements in the matrix is zero.
  Thus, A is the correct choice.

Please comment below if you find anything wrong in the above post.

Question 3

The determinant of the matrix is 

• A. 4
  
• B. 20
  
• C. 0
  
• D. 5
  

Answer: (A)

It is a 4*4 matrix, in the first row all elements except 2 are zero so lets find the cofactor for a(0,0). 

The cofactor has all zeroes except 1 in its first column so lets find the cofactor of a(1,1). 

This turns out to be 2*1 – 6*0 = 2 

a(0,0) * a(1,1) * cofactor(a(1,1)) = 2 * 1 *2 = 4 

Hence the answer is 4. 

Question 4

Let S and T be language over Σ = {a,b} represented by the regular expressions (a+b*)* and (a+b)*, respectively. Which of the following is true?

• A. S ⊂ T
• B. T ⊂ S
• C. S = T
• D. S ∩ T = φ

Answer: (C)

Both have same output because if we draw DFA of S which is (a+b*)*, at final state it is just repeating.

Question 5

Let L denotes the language generated by the grammar S -> 0S0/00. Which of the following is true?

• A. L = 0+
• B. L is regular but not 0+
• C. L is context free but not regular
• D. L is not context free

Answer: (B)

Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0's ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,...}, i.e only even no of  0's ( excluding empty string}.   Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e  α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)   Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+. Option B :  Hence This option is Correct, because L is Regular but not 0+, as we proved above.

Question 6

The number 43 in 2's complement representation is

• A. 01010101
• B. 11010101
• C. 00101011
• D. 10101011

Answer: (C)

In2's complement representation, positive numbers are represented as their representation and negative numbers are represented by first doing 1's complement, then adding 1 to the result. So 43 is represented as 00101011. Note that option represents -43.

Question 7

To put the 8085 microprocessor in the wait state

• A. lower the-HOLD input
• B. lower the READY input
• C. raise the HOLD input
• D. raise the READY input

Answer: (B)

• If ready pin is high the microprocessor will complete the operation and proceeds for the next operation.
• If ready pin is low the microprocessor will wait until it goes high. Thus, option (B) is the answer. Please comment below if you find anything wrong in the above post.

Question 8

Comparing the time T1 taken for a single instruction on a pipelined CPU with time T2 taken on a non­ pipelined but identical CPU, we can say that

• A. T1 <= T2
• B. T1 >= T2
• C. T1 < T2
• D. T1 is T2 plus the time taken for one instruction fetch cycle

Answer: (B)

Pipelining does not increase the execution time of a single instruction. It increases the overall performance by executing instructions in multiple pipeline stages. We assume that each stage takes ‘T’ unit of time both in pipelined and non-pipelined CPU. Let total stages in pipelined CPU = Total stages in non-pipelined CPU = K and number of Instructions = N = 1

• Pipelined CPU : Total time (T1) = (K + (N - 1)) * T = KT
• Non-Pipelined CPU : Total time (T2) = KNT = KT Considering buffer delays in pipelined CPU, T1 >= T2  Thus, option (B) is the answer. Please comment below if you find anything wrong in the above post.

Question 9

The 8085 microprocessor responds to the presence of an interrupt

• A. As soon as the TRAP pin becomes 'high'
• B. By checking the TRAP pin for 'high' status at the end of each instruction fetch
• C. By checking the TRAP pin for 'high' status at the end of the execution of each instruction
• D. By Checking the TRAP pin for 'high' status at regular intervals

Answer: (C)

Explanation: The microprocessor recognizes interrupt request on request lines(RST7.5,RST 5.5,RST 6.5,TRAP,INTR) at the end of current instruction execution. TRAP is non maskable interrupt .TRAP is active high ,level,edge triggered non maskable highest priority interrupt.when TRAP line is active microprocessor insert intervals restarts automatically at vector location of TRAP. So correct option is (C).

Question 10

The most appropriate matching for the following pairs

X: Indirect addressing            1 : Loops

Y: Immediate addressing           2 : Pointers

Z: Auto decrement addressing      3: Constants

is

• A. X-3, Y-2, Z-1
• B. X-I, Y-3, Z-2
• C. X-2, Y-3, Z-1
• D. X-3, Y-l, Z-2

Answer: (C)

Explanation: In Indirect  addressing mode the instruction does not have the address of the data to be operated on,but the instruction points where the address is stored(it is indirectly specifying the address of memory location where the data is stored or to be stored) In immediate addressing mode the data is to be used is immediately given in instruction itself;so it deals with constant data. In Autodecrement addressing mode,  Before determining the effective address, the value in the base register is decremented by the size of the data item which is to be accessed. Within a loop, this addressing mode can be used to step backwards through all the elements of an array or vector. So (C) is correct option.