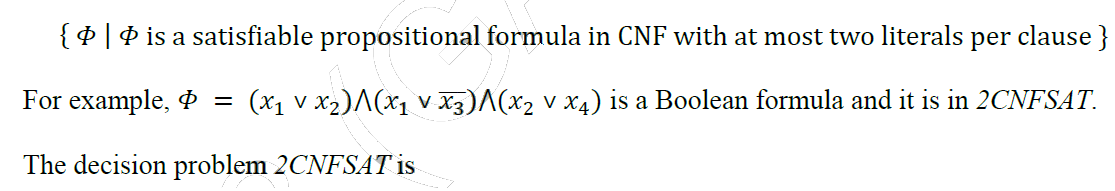Top MCQs on NP Complete Complexity with Answers
Question 1
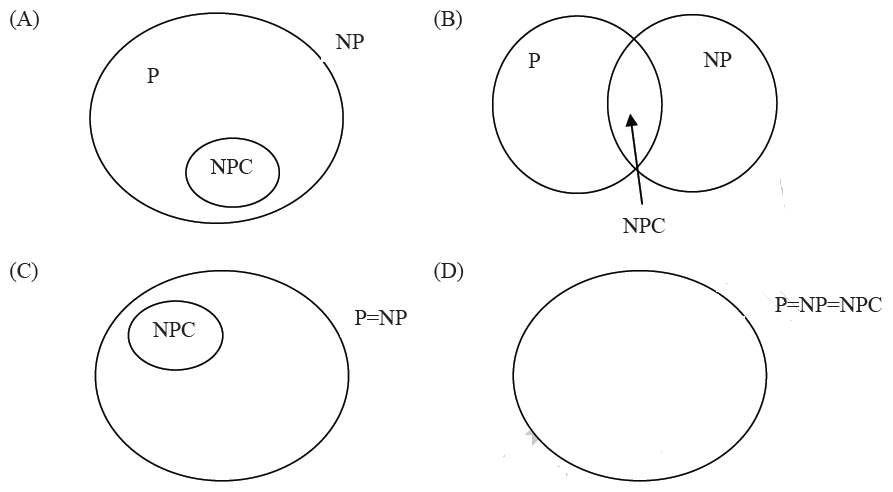
Let S be an NP-complete problem and Q and R be two other problems not known to be in NP. Q is polynomial time reducible to S and S is polynomial-time reducible to R. Which one of the following statements is true? (GATE CS 2006)
Question 2
Let X be a problem that belongs to the class NP. Then which one of the following is TRUE?
Question 4
Which of the following statements are TRUE?
(1) The problem of determining whether there exists a cycle in an undirected graph is in P.
(2) The problem of determining whether there exists a cycle in an undirected graph is in NP.
(3) If a problem A is NP-Complete, there exists a non-deterministic polynomial time algorithm to solve A.
Question 5
Which of the following statements are TRUE?
1. The problem of determining whether there exists a cycle in an undirected graph is in P. 2. The problem of determining whether there exists a cycle in an undirected graph is in NP. 3. If a problem A is NP-Complete, there exists a non-deterministic polynomial time algorithm to solve A.
Question 6
Question 8
Consider the following two problems on undirected graphs
α : Given G(V, E), does G have an independent set of size | V | - 4? β : Given G(V, E), does G have an independent set of size 5?Which one of the following is TRUE?
Question 9
Ram and Shyam have been asked to show that a certain problem Π is NP-complete. Ram shows a polynomial time reduction from the 3-SAT problem to Π, and Shyam shows a polynomial time reduction from Π to 3-SAT. Which of the following can be inferred from these reductions ?
Question 10
Consider two decision problems Q1, Q2 such that Q1 reduces in polynomial time to 3-SAT and 3-SAT reduces in polynomial time to Q2. Then which one of the following is consistent with the above statement?
There are 20 questions to complete.
Last Updated :
Take a part in the ongoing discussion