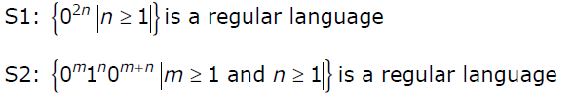GATE-CS-2001

Question 1

Consider the following statements:

S1: The sum of two singular n × n matrices may be non-singular
S2: The sum of two n × n non-singular matrices may be singular. 

Which of the following statements is correct?

• A. S1 and S2 are both true
• B. S1 is true, S2 is false
• C. S1 is false, S2 is true
• D. S1 and S2 are both false

Answer: (A)

Singular Matrix: A square matrix is singular if and only if its determinant value is 0. S1 is True: The sum of two singular n × n matrices may be non-singular It can be seen be taking following example. The following two matrices are singular, but their sum is non-singular.

M1 and M2 are singular
M1 =  1  1
      1  1
       
M2 =   1  -1
      -1   1

But M1+M2 is non-singular  
M1+M2 =  2  0
         0  2

S2 is True: The sum of two n × n non-singular matrices may be singular

M1 and M2 are non-singular
M1 =  1  0
      0  1
       
M2 =   -1  0
        0  -1

But M1+M2 is singular  
M1+M2 =  0  0
         0  0

Question 2

Consider the following relations:

R1(a,b) if (a+b) is even over the set of integers
R2(a,b) if (a+b) is odd over the set of integers
R3(a,b) if a.b > 0 over the set of non-zero rational numbers
R4(a,b) if |a - b| <= 2 over the set of natural numbers

Which of the following statements is correct?

• A. R1 and R2 are equivalence relations, R3 and R4 are not
• B. R1 and R3 are equivalence relations, R2 and R4 are not
• C. R1 and R4 are equivalence relations, R2 and R3 are not
• D. R1, R2, R3 and R4 are all equivalence relations

Answer: (B)

So basically, we have to tell whether these relations are equivalence or not.

1. R1(a,b)
   • Reflexive : Yes, because (a+a) is even.
   • Symmetric : Yes, (a+b) is even ⟹ (b+a) is even.
   • Transitive : Yes, because (a+b) is even and (b+c) is even ⟹ (a+c) is even.
     So R1 is equivalence relation.
     
2. R2(a,b)
   • Reflexive : No, because (a+a) is even.
     So R2 is not equivalence relation.
     
3. R3(a,b)
   • Reflexive : Yes, because a.a > 0.
   • Symmetric : Yes, a.b > 0 ⟹ b.a > 0.
   • Transitive : Yes, because a.b > 0 and b.c > 0 ⟹ a.c > 0.
     So R3 is equivalence relation.
     
4. R4(a,b)
   • Reflexive : Yes, because |a-a| ≤ 2.
   • Symmetric : Yes, |a-b| ≤ 2 ⟹ |b-a| ≤ 2.
   • Transitive : No, because |a-b| ≤ 2 and |b-c| ≤ 2 ⇏ (a-c) is even.
     So R4 is not equivalence relation.

So option (b) is correct.. 

Source: http://www.cse.iitd.ac.in/~mittal/gate/gate_math_2001.html

Question 3

Consider two well-formed formulas in prepositional logic. 

F1 : P ⇒ ¬P
F2 : ( P⇒¬P)∨(¬P⇒P)

Which of the following statements is correct? 

• A. F1 unsatisfiable, F2 is satisfiable
• B. F1 and F2 are both satisfiable
• C. F1 is unsatisfiable, F2 is valid 
• D. F1 is satisfiable, F2 is valid

Answer: (D)

The concept behind this solution is: 
a) Satisfiable 
If there is an assignment of truth values which makes that expression true. 
b) UnSatisfiable 
If there is no such assignment which makes the expression true 
c) Valid 
If the expression is Tautology 
Here, P => Q is nothing but –P v Q 
F1: P => -P = -P v –P = -P 
F1 will be true if P is false and F1 will be false when P is true so F1 is Satisfiable 
F2: (P => -P) v (-P => P) which is equals to (-P v-P) v (-(-P) v P) = (-P) v (P) = 
Tautology 
So, F1 is Satisfiable and F2 is valid 
Option (a) is correct. 

Question 4

Consider the following two statements:

• A. Only S1 is correct
• B. Only S2 is correct
• C. Both S1 and S2 are correct
• D. None of S1 and S2 is correct

Answer: (A)

We can easily build a DFA for S1. All we need to check is whether input string has even number of 0's. Therefore S1 is regular. We can't make a DFA for S2. For S2, we need a stack. Therefore S2 is not regular.

Question 5

Which of the following statements is true?

• A. If a language is context free it can always be accepted by a deterministic push-down automaton
• B. The union of two context free languages is context free
• C. The intersection of two context free languages is context free
• D. The complement of a context free language is context free

Answer: (B)

Refer http://en.wikipedia.org/wiki/Context-free_language#Closure_properties

Question 6

Given an arbitary non-deterministic finite automaton (NFA) with N states, the maximum number of states in an equivalent minimized DFA is at least

• A. N²
• B. 2^N
• C. 2N
• D. N!

Answer: (B)

Refer http://en.wikipedia.org/wiki/Powerset_construction

Question 7

More than one word are put in one cache block to

• A. exploit the temporal locality of reference in a program
• B. exploit the spatial locality of reference in a program
• C. reduce the miss penalty
• D. none of the above

Answer: (B)

See question 3 of http://www.geeksforgeeks.org/operating-systems-set-2/

Question 8

Which of the following statements is false?

• A. Virtual memory implements the translation of a program‘s address space into physical memory address space
• B. Virtual memory allows each program to exceed the size of the primary memory
• C. Virtual memory increases the degree of multiprogramming
• D. Virtual memory reduces the context switching overhead

Answer: (D)

See question 4 of http://www.geeksforgeeks.org/operating-systems-set-2/

Question 9

A low memory can be connected to 8085 by using

• A. INTER
• B. RESET IN
• C. HOLD
• D. READY

Answer: (D)

A low memory can be connected to 8085 by using READY signal, Communication is only possible when READY signal is set .So (D) is correct option

Question 10

Suppose a processor does not have any stack pointer register. Which of the following statements is true?

• A. It cannot have subroutine call instruction
• B. It can have subroutine call instruction, but no nested subroutine calls
• C. Nested subroutine calls are possible, but interrupts are not
• D. All sequences of subroutine calls and also interrupts are possible

Answer: (A)

Stack pointer register hold the address of top of stack, which is the location of memory at which CPU should resume its execution after servicing some interrupt or subroutine call. So if SP register is not available then no subroutine call instructions are possible. So (A) is correct option.