Top MCQs on Algorithms in DSA with Answers
Question 1
Given 8 identical coins out of which one coin is heavy and a pan balance. How many minimum number of measurements are needed to find the heavy coin?
Question 2
In a village, people build houses in the same side of the road. A thief plans to loot the village. He wants maximum amount of money without having any risk of getting caught. By some means, the villagers know that their adjacent house is being looted or not and thus they become alert. So the thief cannot loot contiguous two houses. Given that the thief knows the amount of money stored in each house and the road is straight and there is no turning, which is the most efficient algorithmic strategy to solve this problem?
Question 4
A set X can be represented by an array x[n] as follows:
[caption width="800"]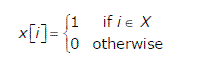 [/caption]
[/caption]
Consider the following algorithm in which x,y, and z are Boolean arrays of size n:
algorithm zzz(x[] , y[], z [])
{
int i;
for (i=O; i<n; ++i)
z[i] = (x[i] ^ ~y[i]) V (~x[i] ^ y[i]) }
The set Z computed by the algorithm is:
Question 5
An element in an array X is called a leader if it is greater than all elements to the right of it in X. The best algorithm to find all leaders in an array (GATE CS 2006)
Question 6
Consider the following C function.
c
For large values of y, the return value of the function f best approximates (GATE CS 2003)
float f(float x, int y)
{
float p, s; int i;
for (s=1, p=1, i=1; i < y; i ++)
{
p*= x/i;
s+=p;
}
return s;
}
Question 7
Suppose you are given an array s[1...n] and a procedure reverse (s,i,j) which reverses the order of elements in a between positions i and j (both inclusive). What does the following sequence
do, where 1 < k <= n: reverse (s, 1, k); reverse (s, k + 1, n); reverse (s, 1, n);(GATE CS 2000)
Question 8
An inversion in a an array A[] is a pair (A[i], A[j]) such that A[i] > A[j] and i < j. An array will have maximum number of inversions if it is:
Question 9
The procedure given below is required to find and replace certain characters inside an input character string supplied in array A. The characters to be replaced are supplied in array oldc, while their respective replacement characters are supplied in array newc. Array A has a fixed length of five characters, while arrays oldc and newc contain three characters each. However, the procedure is flawed
void find_and_replace(char *A, char *oldc, char *newc) {
for (int i = 0; i < 5; i++)
for (int j = 0; j < 3; j++)
if (A[i] == oldc[j]) A[i] = newc[j];
}
The procedure is tested with the following four test cases
(1) oldc = "abc", newc = "dab"
(2) oldc = "cde", newc = "bcd"
(3) oldc = "bca", newc = "cda"
(4) oldc = "abc", newc = "bac"
The tester now tests the program on all input strings of length five consisting of characters ‘a’, ‘b’, ‘c’, ‘d’ and ‘e’ with duplicates allowed. If the tester carries out this testing with the four test cases given above, how many test cases will be able to capture the flaw?
Question 10
In the above question, if array A is made to hold the string “abcde”, which of the above four test cases will be successful in exposing the flaw in this procedure?
There are 49 questions to complete.
Last Updated :
Take a part in the ongoing discussion