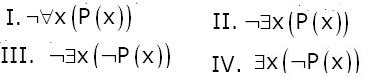Propositional and First Order Logic.
Question 1
Negation of the proposition
[caption width="800"] [/caption]
[/caption]
is:
[caption width="800"] [/caption]
[/caption]Question 2
Question 4
What is the correct translation of the following statement into mathematical logic? “Some real numbers are rational”
[caption width="800"] [/caption]
[/caption]Question 5
Which one of the following options is CORRECT given three positive integers x, y and z, and a predicate?
P(x) = ¬(x=1)∧∀y(∃z(x=y*z)⇒(y=x)∨(y=1))
Question 6
Suppose the predicate F(x, y, t) is used to represent the statement that person x can fool person y at time t. which one of the statements below expresses best the meaning of the formula ∀x∃y∃t(¬F(x, y, t))?
Question 7
Which one of the following is the most appropriate logical formula to represent the statement? "Gold and silver ornaments are precious".
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious
Question 8
The binary operation ? is defined as follows
P | Q | P?Q |
T | T | T |
T | F | T |
F | T | F |
F | F | T |
Which one of the following is equivalent to P∨Q?
Question 10
Let fsa and pda be two predicates such that fsa(x) means x is a finite state automaton, and pda(y) means that y is a pushdown automaton. Let equivalent be another predicate such that equivalent (a, b) means a and b are equivalent. Which of the following first order logic statements represents the following:
Each finite state automaton has an equivalent pushdown automaton.
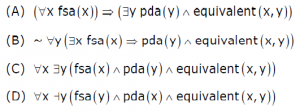
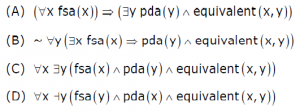
There are 89 questions to complete.
Last Updated :
Take a part in the ongoing discussion