Top MCQs on Shortest Paths in Graphs with Answers

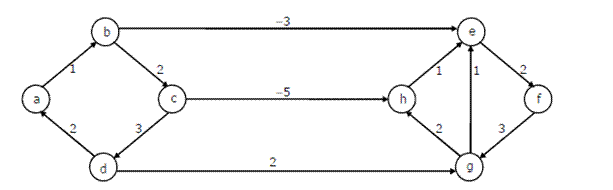
Question 1

Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices S and T. Which one will be reported by Dijstra?s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered.

• SDT
• SBDT
• SACDT
• SACET

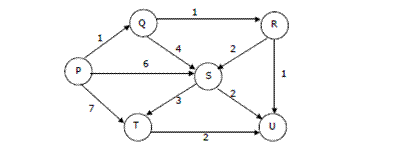
Question 2

To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:

• Queue
• Stack
• Heap
• B-Tree

Question 3

Dijkstra’s single source shortest path algorithm when run from vertex a in the below graph, computes the correct shortest path distance to

• only vertex a
• only vertices a, e, f, g, h
• only vertices a, b, c, d
• all the vertices

Question 4

In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity by

• Dijkstra’s algorithm starting from S.
• Warshall’s algorithm
• Performing a DFS starting from S.
• Performing a BFS starting from S.

Question 5

Suppose we run Dijkstra’s single source shortest-path algorithm on the following edge weighted directed graph with vertex P as the source. In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized? (GATE CS 2004)

• P, Q, R, S, T, U
• P, Q, R, U, S, T
• P, Q, R, U, T, S
• P, Q, T, R, U, S

Question 6

What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices?

• Θ(V²)

• Θ(V² log v)

• Θ(V³)

• Θ(V³ log v)

Question 7

In a weighted graph, assume that the shortest path from a source \'s\' to a destination \'t\' is correctly calculated using a shortest path algorithm. Is the following statement true? If we increase weight of every edge by 1, the shortest path always remains same.

• Yes
• No

Question 8

Following statement is true or false?

If we make following changes to  Dijkstra, then it can be used to find 
the longest simple path, assume that the graph is acyclic.

1) Initialize all distances as minus infinite instead of plus infinite.

2) Modify the relax condition in  Dijkstra\'s algorithm to update distance
  of an adjacent v of the currently considered vertex u only
  if "dist[u]+graph[u][v] > dist[v]". In shortest path algo, 
  the sign is opposite. 

• True
• False

Question 9

Which of the following algorithm can be used to efficiently calculate single source shortest paths in a Directed Acyclic Graph?

• Dijkstra
• Bellman-Ford
• Topological Sort
• Strongly Connected Component

Question 10

Is the following statement valid about shortest paths? Given a graph, suppose we have calculated shortest path from a source to all other vertices. If we modify the graph such that weights of all edges is becomes double of the original weight, then the shortest path remains same only the total weight of path changes.

• True
• False