Dice Throw | DP-30
Last Updated :
06 Oct, 2023
Given n dice each with m faces, numbered from 1 to m, find the number of ways to get sum X. X is the summation of values on each face when all the dice are thrown.
The Naive approach is to find all the possible combinations of values from n dice and keep on counting the results that sum to X.
This problem can be efficiently solved using Dynamic Programming (DP).
Let the function to find X from n dice is: Sum(m, n, X)
The function can be represented as:
Sum(m, n, X) = Finding Sum (X - 1) from (n - 1) dice plus 1 from nth dice
+ Finding Sum (X - 2) from (n - 1) dice plus 2 from nth dice
+ Finding Sum (X - 3) from (n - 1) dice plus 3 from nth dice
...................................................
...................................................
...................................................
+ Finding Sum (X - m) from (n - 1) dice plus m from nth dice
So we can recursively write Sum(m, n, x) as following
Sum(m, n, X) = Sum(m, n - 1, X - 1) +
Sum(m, n - 1, X - 2) +
.................... +
Sum(m, n - 1, X - m)
Why DP approach?
The above problem exhibits overlapping subproblems. See the below diagram. Also, see this recursive implementation. Let there be 3 dice, each with 6 faces and we need to find the number of ways to get sum 8:
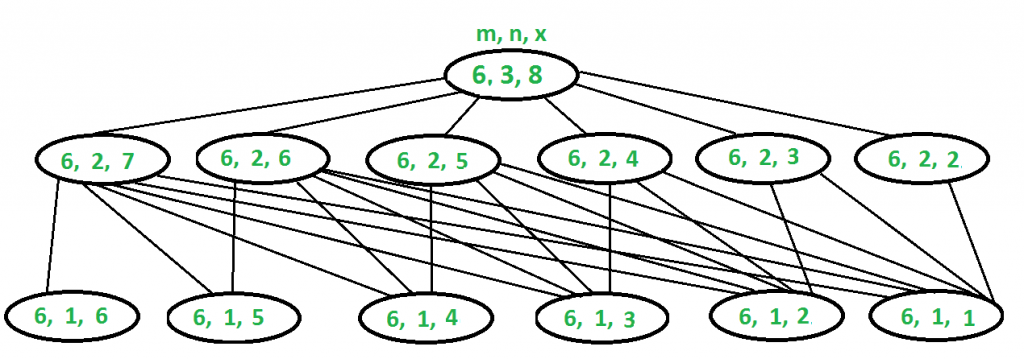
Sum(6, 3, 8) = Sum(6, 2, 7) + Sum(6, 2, 6) + Sum(6, 2, 5) +
Sum(6, 2, 4) + Sum(6, 2, 3) + Sum(6, 2, 2)
To evaluate Sum(6, 3, 8), we need to evaluate Sum(6, 2, 7) which can
recursively written as following:
Sum(6, 2, 7) = Sum(6, 1, 6) + Sum(6, 1, 5) + Sum(6, 1, 4) +
Sum(6, 1, 3) + Sum(6, 1, 2) + Sum(6, 1, 1)
We also need to evaluate Sum(6, 2, 6) which can recursively written
as following:
Sum(6, 2, 6) = Sum(6, 1, 5) + Sum(6, 1, 4) + Sum(6, 1, 3) +
Sum(6, 1, 2) + Sum(6, 1, 1)
..............................................
..............................................
Sum(6, 2, 2) = Sum(6, 1, 1)
Please take a closer look at the above recursion. The sub-problems in RED are solved first time and sub-problems in BLUE are solved again (exhibit overlapping sub-problems). Hence, storing the results of the solved sub-problems saves time.
Following is implementation of Dynamic Programming approach.
C++
#include <iostream>
#include <string.h>
using namespace std;
int findWays(int m, int n, int x)
{
int table[n + 1][x + 1];
memset(table, 0, sizeof(table));
for (int j = 1; j <= m && j <= x; j++)
table[1][j] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j <= x; j++)
for (int k = 1; k <= m && k < j; k++)
table[i][j] += table[i-1][j-k];
return table[n][x];
}
int main()
{
cout << findWays(4, 2, 1) << endl;
cout << findWays(2, 2, 3) << endl;
cout << findWays(6, 3, 8) << endl;
cout << findWays(4, 2, 5) << endl;
cout << findWays(4, 3, 5) << endl;
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class GFG {
public static long findWays(int m, int n, int x){
long[][] table = new long[n+1][x+1];
for(int j = 1; j <= m && j <= x; j++)
table[1][j] = 1;
for(int i = 2; i <= n;i ++){
for(int j = 1; j <= x; j++){
for(int k = 1; k < j && k <= m; k++)
table[i][j] += table[i-1][j-k];
}
}
return table[n][x];
}
public static void main (String[] args) {
System.out.println(findWays(4, 2, 1));
System.out.println(findWays(2, 2, 3));
System.out.println(findWays(6, 3, 8));
System.out.println(findWays(4, 2, 5));
System.out.println(findWays(4, 3, 5));
}
}
|
Python3
def findWays(m,n,x):
table=[[0]*(x+1) for i in range(n+1)]
for j in range(1,min(m+1,x+1)):
table[1][j]=1
for i in range(2,n+1):
for j in range(1,x+1):
for k in range(1,min(m+1,j)):
table[i][j]+=table[i-1][j-k]
return table[-1][-1]
print(findWays(4,2,1))
print(findWays(2,2,3))
print(findWays(6,3,8))
print(findWays(4,2,5))
print(findWays(4,3,5))
|
C#
using System;
class GFG
{
static int findWays(int m,
int n, int x)
{
int[,] table = new int[n + 1,
x + 1];
for (int i = 0; i <= n; i++)
for (int j = 0; j <= x; j++)
table[i, j] = 0;
for (int j = 1;
j <= m && j <= x; j++)
table[1, j] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j <= x; j++)
for (int k = 1;
k <= m && k < j; k++)
table[i, j] += table[i - 1,
j - k];
return table[n, x];
}
public static void Main()
{
Console.WriteLine(findWays(4, 2, 1));
Console.WriteLine(findWays(2, 2, 3));
Console.WriteLine(findWays(6, 3, 8));
Console.WriteLine(findWays(4, 2, 5));
Console.WriteLine(findWays(4, 3, 5));
}
}
|
PHP
<?php
function findWays($m, $n, $x)
{
$table;
for ($i = 1; $i < $n + 1; $i++)
for ($j = 1; $j < $x + 1; $j++)
$table[$i][$j] = 0;
for ($j = 1; $j <= $m &&
$j <= $x; $j++)
$table[1][$j] = 1;
for ($i = 2; $i <= $n; $i++)
for ($j = 1; $j <= $x; $j++)
for ($k = 1; $k <= $m &&
$k < $j; $k++)
$table[$i][$j] +=
$table[$i - 1][$j - $k];
return $table[$n][$x];
}
echo findWays(4, 2, 1). "\n";
echo findWays(2, 2, 3). "\n";
echo findWays(6, 3, 8). "\n";
echo findWays(4, 2, 5). "\n";
echo findWays(4, 3, 5). "\n";
?>
|
Javascript
<script>
function findWays(m,n,x)
{
let table = new Array(n+1);
for(let i=0;i<(n+1);i++)
{
table[i]=new Array(x+1);
for(let j=0;j<(x+1);j++)
{
table[i][j]=0;
}
}
for(let j = 1; j <= m && j <= x; j++)
table[1][j] = 1;
for(let i = 2; i <= n;i ++){
for(let j = 1; j <= x; j++){
for(let k = 1; k < j && k <= m; k++)
table[i][j] += table[i-1][j-k];
}
}
return table[n][x];
}
document.write(findWays(4, 2, 1)+"<br>");
document.write(findWays(2, 2, 3)+"<br>");
document.write(findWays(6, 3, 8)+"<br>");
document.write(findWays(4, 2, 5)+"<br>");
document.write(findWays(4, 3, 5)+"<br>");
</script>
|
Output :
0
2
21
4
6
Time Complexity: O(m * n * x) where m is number of faces, n is number of dice and x is given sum.
Auxiliary Space: O(n * x)
We can add the following two conditions at the beginning of findWays() to improve performance of the program for extreme cases (x is too high or x is too low)
C++
if (m*n <= x)
return (m*n == x);
if (n >= x)
return (n == x);
|
Java
if (m*n <= x)
return (m*n == x);
if (n >= x)
return (n == x);
|
Python3
def condition(m, n, x):
if (m*n <= x):
return (m*n == x)
if (n >= x):
return (n == x)
|
C#
if (m*n <= x)
return (m*n == x);
if (n >= x)
return (n == x);
|
Javascript
if (m*n <= x)
return (m*n == x);
if (n >= x)
return (n == x);
|
With above conditions added, time complexity becomes O(1) when x >= m*n or when x <= n.
Following is the implementation of the Optimized Dynamic Programming approach.
C++
#include<bits/stdc++.h>
using namespace std;
long findWays(int f, int d, int s)
{
long mem[d + 1][s + 1];
memset(mem,0,sizeof mem);
mem[0][0] = 1;
for (int i = 1; i <= d; i++)
{
for (int j = i; j <= s; j++)
{
mem[i][j] = mem[i][j - 1] + mem[i - 1][j - 1];
if (j - f - 1 >= 0)
mem[i][j] -= mem[i - 1][j - f - 1];
}
}
return mem[d][s];
}
int main(void)
{
cout << findWays(4, 2, 1) << endl;
cout << findWays(2, 2, 3) << endl;
cout << findWays(6, 3, 8) << endl;
cout << findWays(4, 2, 5) << endl;
cout << findWays(4, 3, 5) << endl;
return 0;
}
|
Java
/**
* The main function that returns number of ways to get sum 'x'
* with 'n' dice and 'm' with m faces.
*
*/
public class GFG {
public static long findWays(int f, int d, int s) {
long mem[][] = new long[d + 1][s + 1];
mem[0][0] = 1;
for(int i=1; i<=d; i++) {
for(int j=i; j<=s; j++) {
mem[i][j] = mem[i][j-1] + mem[i-1][j-1];
if(j-f-1 >= 0)
mem[i][j] -= mem[i-1][j-f-1];
}
}
return mem[d][s];
}
public static void main(String[] args) {
System.out.println(findWays(4, 2, 1));
System.out.println(findWays(2, 2, 3));
System.out.println(findWays(6, 3, 8));
System.out.println(findWays(4, 2, 5));
System.out.println(findWays(4, 3, 5));
}
}
|
Python3
def findWays(f, d, s):
mem = [[0 for i in range(s+1)] for j in range(d+1)]
mem[0][0] = 1
for i in range(1, d+1):
for j in range(1, s+1):
mem[i][j] = mem[i][j - 1] + mem[i - 1][j - 1]
if j - f - 1 >= 0:
mem[i][j] -= mem[i - 1][j - f - 1]
return mem[d][s]
print(findWays(4, 2, 1))
print(findWays(2, 2, 3))
print(findWays(6, 3, 8))
print(findWays(4, 2, 5))
print(findWays(4, 3, 5))
|
C#
using System;
class GFG
{
public static long findWays(int f, int d, int s)
{
long [,]mem = new long[d + 1,s + 1];
mem[0,0] = 1;
for(int i = 1; i <= d; i++)
{
for(int j = i; j <= s; j++)
{
mem[i,j] = mem[i,j-1] + mem[i-1,j-1];
if(j-f-1 >= 0)
mem[i,j] -= mem[i-1,j-f-1];
}
}
return mem[d,s];
}
public static void Main(String[] args)
{
Console.WriteLine(findWays(4, 2, 1));
Console.WriteLine(findWays(2, 2, 3));
Console.WriteLine(findWays(6, 3, 8));
Console.WriteLine(findWays(4, 2, 5));
Console.WriteLine(findWays(4, 3, 5));
}
}
|
Javascript
<script>
function findWays(f, d, s)
{
let mem = new Array(d + 1);
for(let i = 0; i < (d + 1); i++)
{
mem[i] = new Array(s + 1);
for(let j = 0; j < s + 1; j++)
{
mem[i][j] = 0;
}
}
mem[0][0] = 1;
for(let i = 1; i <= d; i++)
{
for(let j = i; j <= s; j++)
{
mem[i][j] = mem[i][j - 1] + mem[i - 1][j - 1];
if (j - f - 1 >= 0)
mem[i][j] -= mem[i - 1][j - f - 1];
}
}
return mem[d][s];
}
document.write(findWays(4, 2, 1) + "<br>");
document.write(findWays(2, 2, 3) + "<br>");
document.write(findWays(6, 3, 8) + "<br>");
document.write(findWays(4, 2, 5) + "<br>");
document.write(findWays(4, 3, 5) + "<br>");
</script>
|
Output :
0
2
21
4
6
Time Complexity: O(n * x) where n is number of dice and x is given sum.
Space Complexity: O(n * x) where n is number of dice and x is given sum.
Exercise:
Extend the above algorithm to find the probability to get Sum > X.
This article is compiled by Aashish Barnwal.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...