Graph theory | GATE PYQ [2010-2025]

Last Updated :

Discuss

Comments

Question 1

The chromatic number of the following graph is _______. [ NAT || GATE 2018 || 1 Marks]

• 3

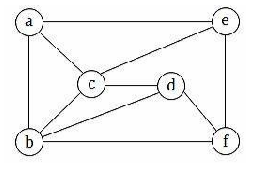
Question 2

The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. The chromatic number of the following graph is ______. [ NAT || GATE 2024 Set-2 || 2 Marks ]

• 2

Question 3

The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. Let G be any graph with n vertices and chromatic number k. Which of the following statements is/are always TRUE? [ MSQ || GATE 2024 Set-1 || 2 Marks]

• G contains a complete subgraph with k vertices.

• G contains an independent set of size at least n/k.

• G contains at least k(k−1)/2 edges.

• G contains a vertex of degree at least k.

Question 4

Let G be a simple, finite, undirected graph with vertex set {v₁,...,v_n}.

Let Δ(G) denote the maximum degree of G and let N = {1, 2,...} denote the set of all possible colors. Color the vertices of G using the following greedy strategy:

for i = 1,...,n

color(v_i) ← min {j ∈ N : no neighbour of v_i is colored j}

Which of the following statements is/are TRUE?[ MSQ || GATE 2023 || 2 Marks]

• This procedure results in a proper vertex coloring of G.

• The number of colors used in at most Δ (G) + 1.

• The number of colors used is at most Δ (G).

• The number of colors used is equal to the chromatic number of G.

Question 5

Let G(V, E) be a directed graph, where V = {1, 2, 3, 4, 5} is the set of vertices and E is the set of directed edges, as defined by the following adjacency matrix A.

A[i][j] = 1, 1 ≤ j ≤ i ≤ 5

A[i][j] = 0, otherwise

A[i][j] = 1 indicates a directed edge from node i to node j. A directed spanning tree of G, rooted at r ∈ V, is defined as a subgraph T of G such that the undirected version of T is a tree, and T contains a directed path from r to every other vertex in V. The number of such directed spanning trees rooted at vertex 5 is ____________. [ NAT || GATE 2022 || 2 Marks]

• 24

Question 6

Consider a simple undirected graph of 10 vertices.

If the graph is disconnected, then the maximum number of edges it can have is ____ .[ NAT || GATE 2022 || 2 Marks]

• 36

Question 7

Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices? [ MCQ || GATE 2022 || 2 Marks]

• The diagonal entries of A² are the degrees of the vertices of the graph.

• If the graph is connected, then none of the entries of A^n- ¹ + Iₙ can be zero.

• If the sum of all the elements of A is at most 2(n-1), then the graph must be acyclic.

• If there is at least a 1 in each of A’s rows and columns, then the graph must be connected.

Question 8

Consider a simple undirected unweighted graph with at least three vertices. If A is the adjacency matrix of the graph, then the number of 3-cycles in the graph is given by the trace of ___. [ MCQ || GATE 2022 || 2 Marks]

• A³

• A³ divided by 2

• A³ divided by 3

• A³ divided by 6

Question 9

Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three? [ MCQ || GATE 2013 || 1 Marks ]

• 1/8

• 1

• 7

• 8

Question 10

Consider the following directed graph:

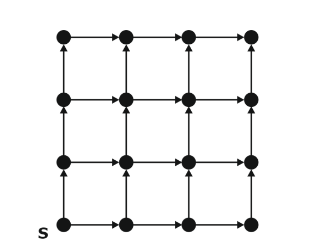
Which of the following is/are correct about the graph? [ MSQ || GATE 2021 Set-2 || 2 Marks ]

• The graph does not have a strongly connected component.

• The graph does not have a topological order.

• A depth-first traversal starting at vertex S classifies three directed edges as back edges.

• For each pair of vertices u and v, there is a directed path from u to v.

Tags:

GATE CS

GATE

Discrete Mathematics