Translations of Functions

Translation of a function involves shifting its graph in the coordinate plane without altering its shape. This transformation moves every point of the graph of the function by the same amount. It is achieved by adding or subtracting the constants to the function's input or output.

Mathematically, if f(x) is a function, then:

• Horizontal Translation:
  • f(x − h) represents a shift to the right by h units.
  • f(x + h) represents a shift to the left by h units.

• Vertical Translation:
  • f(x) + k represents a shift upward by k units.
  • f(x) − k for a shift downward by k units.

Horizontal Translations

Translating f(x) by h units horizontally results in the f(x − h). A positive h shifts the graph to the right and a negative h shifts it to the left.

• Rightward Translation: Adding a constant to the input shifts the graph to the right.
  • Function Form: f(x − h)
  • Example: f(x) = x² becomes f(x − 4) = (x − 4)² (shifts the graph of x² right by 4 units).
• Leftward Translation: Subtracting a constant from the input shifts the graph to the left.
  • Function Form: f(x + h)
  • Example: f(x) = x² becomes f(x +3) = (x + 3)² (shifts the graph of x² left by 3 units).

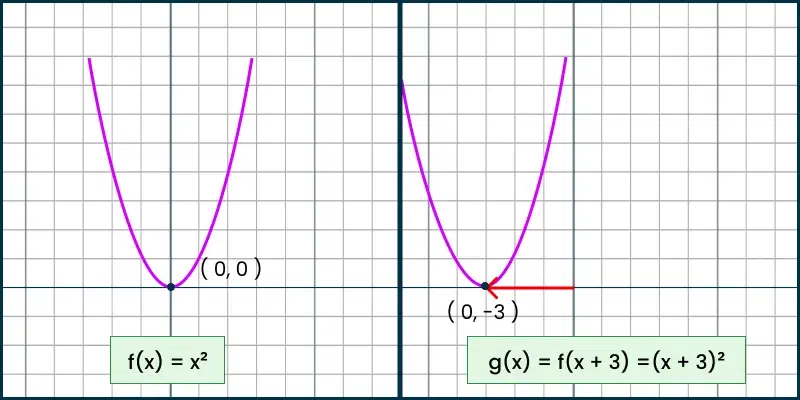
Vertical Translations

Translating f(x) by k units vertically results in f(x)+k. A positive k shifts the graph upwards and a negative k shifts it downwards.

• Upward Translation: Adding a constant to the function translates the graph upward.
  • Function Form: f(x) + k
  • Example: f(x) = x² becomes f(x) + 3 = x² + 3 (shifts the graph of x² up by 3 units).

• Downward Translation: Subtracting a constant from the function translates the graph downward.
  • Function Form: f(x) − k
  • Example: f(x) = x² becomes f(x) − 2 = x² − 2 (shifts the graph of x² down by 2 units).

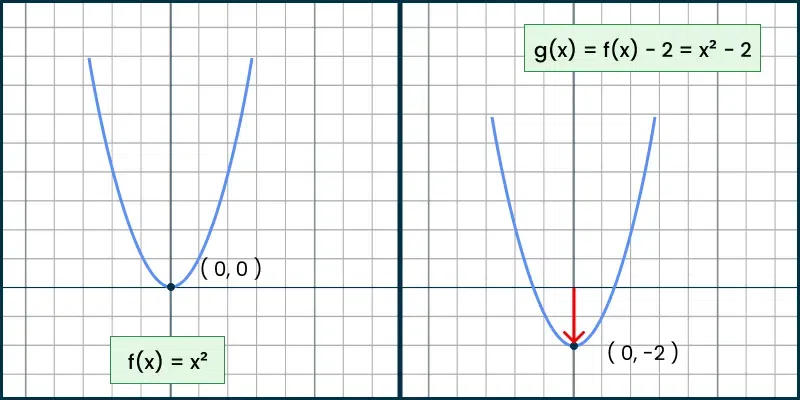
Combined Translations

You can combine both vertical and horizontal translations in one function:

• Function Form: f(x − h) + k
• Example: For f(x) = x², the function f(x − 2) + 1 = (x − 2)² + 3 shifts the graph right by 2 units and up by 3 in.

This results in a parabola with its vertex at (2, 3).

Solved Examples of Translations of Functions

Question 1: Translate the function f(x)= 2x/3 horizontally to the right by 3 units.

Solution:

To translate a function to the right, you subtract from the input x. Thus, the translated function is:

g(x) = f(x−3) = 2x/3 - 3 = (2x - 9)/3

Question 2: Translate the function f(x) = x³ -2x vertically upwards by 4 units.

Solution:

To translate a function upwards, you add to the output. Thus, the translated function is:

g(x) = f(x) + 4 = x³ -2x + 4

Question 3: Translate the function f(x)=x horizontally to the left by 2 units and vertically downwards by 1 unit.

Solution:

• Horizontal translation left: f(x + 2)
• Vertical translation down: Subtract 1 from the output.

Thus, the combined translation is:

g(x) = f(x+2) − 1 = x + 2 − 1 = x + 2

Question 4: Translate the function f(x)=∣x∣ horizontally to the right by 5 units and vertically upwards by 2 units.

Solution:

• Horizontal translation right: f(x − 5)
• Vertical translation up: Add 2 to the output.

The translated function is:

g(x) = f(x − 5) + 2 = ∣x − 5∣ + 2

Question 5: Translate the function f(x) = sin⁡(x) horizontally to the left by π/4​ units and vertically downwards by 1 unit.

Solution:

• Horizontal translation left: f(x + π/4)
• Vertical translation down: Subtract 1 from the output.

Thus, the translated function is:

g(x)=f(x + π/4) − 1 = sin⁡(x + π/4) − 1