Compound interest is an interest that you earn on both the money you originally saved (called "Principal Amount") and any interest you've already earned. Let’s understand how it works with the help of given below Example -
Suppose you put ₹10,000 in a bank account with a 10% annual interest rate that compounds yearly.
Year 1: You start with ₹10,000. After a year, the bank adds 10% interest, which is ₹1,000. So, now you have ₹10,000 + ₹1,000 = ₹11,000.
Year 2: You now have ₹11,000. This year, the bank adds 10% interest on ₹11,000, which is ₹1,100. Now, you have ₹11,000 + ₹1,100 = ₹12,100. Notice the interest is a bit higher because it’s calculated on the full ₹11,000, not just the original ₹10,000.
Year 3: Now, you have ₹12,100. The bank gives you 10% interest on this amount, which is ₹1,210. Now, you have ₹12,100 + ₹1,210 = ₹13,310.
Each year, the interest amount gets a little bigger because you’re earning interest on the interest from previous years, as well as on the original amount. Over time, this makes your money grow much faster.
Tricks Related to Compound Interest
1. Use Direct Formula to Calculate Compound Interest
The compound interest formula is:
A = P (1 + r/n)nt
CI = A – P
Where:
- A = the future value of the investment/loan, including interest.
- P = the principal investment amount (the initial deposit or loan amount).
- r = the annual interest rate (decimal).
- n = the number of times that interest is compounded per unit t.
- t = is the number of years the money is invested or borrowed.
- CI = Compound Interest.
Note: Compound interest grows faster than simple interest because it builds on previously earned interest.
2. Pascal Triangle Trick for Compound Interest
Pascal's Triangle provides coefficients for expanding binomial terms, which can simplify compound interest calculations.
Steps for Pascal's Triangle Trick for Compound Interest
- Get Pascal's Triangle Coefficients:
- Use the row corresponding to the number of years (t).
- Ignore the first "1" (it represents the principal).
- Calculate Successive Interests:
- First year: Interest on the principal.
- Second year: Interest on the first year's interest.
- Third year (and beyond): Continue calculating interest on the previous year’s interest.
- Multiply by Coefficients:
- Multiply each year's interest by its respective coefficient from Pascal's Triangle.
- Sum the Results:
- Add all the products to get the total compound interest.
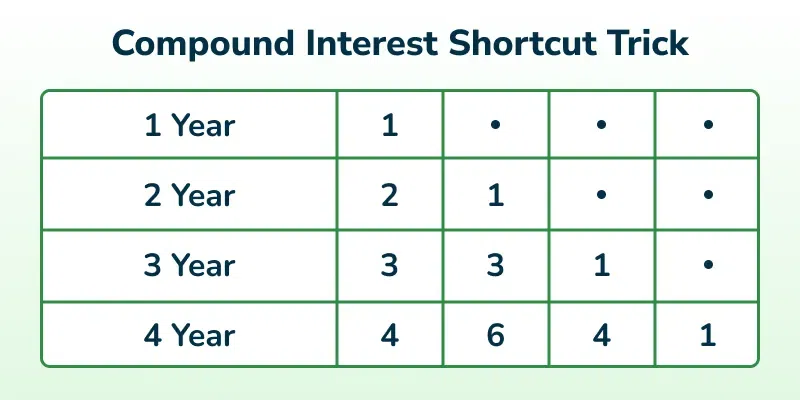
Example:
Let's say we have:
- Principal (P) = Rs: 6000
- Rate (r) = 10% per annum
- Time (t) = 3 years
Solution:
For 3 year the coefficients of 3rd row of Pascal's are: 3 3 1, Ignore the first "1" as it represents the principal amount.
Calculate Sucessive Interests:
First year:
Calculate the 10% of 6000 = 6000 × 10/100 = 600Second year:
Calculate the 10% of 600 = 600 × 10/100 = 60Third year:
Calculate the 10% of 60 = 60 × 10/100 = 6Multiplying the answer with the respective coefficient of Pascal's Triangle:
- (3 × 600) = 1800
- (3 × 60) = 180
- (1 × 6) = 6
Sum the Results:
1800 + 180 + 6 = 1986.Hence, the compound interest for 3 years is 1986.
3. Compound Interest with Different Compounding Frequencies -
Here’s a table with formulas for various compounding frequencies:
Compounding Frequency | Effective Rate per Period | Number of Periods (Time) | Formula |
|---|---|---|---|
Half-Yearly | R/2% | 2t | A = P (1 + R/200)2t |
Quarterly | R/4% | 4t | A = P(1 + R/400)4t |
Monthly | R/12% | 12t | A = P[1 + (R/1200)]12t |
Daily | R/365% | 365t | A = P[1 + (R/36500)]365t |
4. Rule of 72
The Rule of 72 is a quick formula used to estimate how long it will take for an investment to double if compounded annually. This rule provides an approximate time frame based on the interest rate.
Formula
To find the number of years (N) for your money to double: N = 72/r
Example: Let's say you invest Rs 10,000 at an interest rate of 6% compounded annually. In how many years will the amount be doubled?
Solution:
Using the Rule of 72, you can estimate how many years it will take for this investment to double.
Calculation
- Formula: N = 72/r
- Interest Rate (r): 6%
- N = 72/6 = 12 years
It will take approximately 12 years for your Rs 10,000 to double to Rs 20,000 at a 6% annual compounding rate.
Note: The Rule of 72 can also be applied to estimate how long it will take for the value of an asset to halve if it depreciates annually at r%.
5. Compound Interest with Different Rates Each Year
When the interest rates vary each year, for example, with rates of R1%, R2%, and R3% for the 1st, 2nd, and 3rd years respectively, the compound amount can be calculated as follows:
Formula
This formula multiplies each year's growth factor, reflecting the different rates applied consecutively.
Amount = P × (1 + R1/100) × (1 + R2/100) × (1 + R3/100)
6. Formulas for CI-SI Difference Over 2 and 3 Years
For two years, the difference between compound interest and simple interest can be calculated as:
P × R2/1002
For three years, the difference between compound interest and simple interest can be calculated as:
(P × R2/1002) × (R/100 + 3)
7. Compound Interest Timing Shortcut
This trick helps determine the time required for an investment to grow to a specified multiple under compound interest when given a prior growth period. We can use the formula:
(x)1/a = (y)1/b
Where:
- x is the first multiple achieved in years.
- y is the target multiple we want to reach.
- b is the time in years to reach the target multiple y.
Example: An initial sum of money becomes 3 times its original amount in 5 years. How long will it take for this sum to grow to 27 times its original value?
Solution:
Using the shortcut formula:
(x)1/a = (y)1/b
Substitute the given values: x = 3, a = 5, y = 27, and solve for b.
(3)1/5 = (27)1/b
(3)1/5 = (33)1/b
(3)1/5 = (3)3/b
1/5 = 3/bb = 15
It will take 15 years for the initial sum to grow to 27 times its original amount.
8. Compound Interest Annual Growth Rate Shortcut
It’s used to quickly determine the annual compound interest rate when you know how much an investment grows from one year to the next.
If an amount grows to A in N years and then to B in N + 1 years under compound interest, the annual rate of interest R% can be calculated with this shortcut formula:
R% = B − A/A × 100
This formula provides a quick way to estimate the interest rate based on the growth of the investment over consecutive years.
Also Check:
Compound Interest - Questions and Answers
Question 1 : If Rs. 5000 amounts to Rs. 5832 in two years compounded annually, find the rate of interest per annum.
Solution:
Here, P = 5000, A = 5832, n = 2
A = P [1 + (R / 100)]
=> 5832 = 5000 [1 + (R / 100)]
=> [1 + (R / 100)]
= 5832 / 5000
=> [1 + (R / 100)]
= 11664 / 10000
=> [1 + (R / 100)] = 108 / 100
=> R / 100 = 8 / 100
=> R = 8 %
Thus, the required rate of interest per annum in 8 %
Question 2 : The difference between the SI and CI on a certain sum of money at a 10 % rate of annual interest for 2 years is Rs. 549. Find the sum.
Solution :
Let the sum be P.
R = 10 %
n = 2 years
SI = P x R x n / 100 = P x 10 x 2 / 100 = 0.20 P
CI = A - P = P [1 + (R / 100)]
- P = 0.21 P
Now, it is given that CI - SI = 549
=> 0.21 P - 0.20 P = 549
=> 0.01 P = 549
=> P = 54900
Therefore, the required sum of money is Rs. 54,900
Question 3 : A sum of Rs. 1000 is to be divided among two brothers such that if the interest being compounded annually is 5 % per annum, then the money with the first brother after 4 years is equal to the money with the second brother after 6 years.
Solution :
Let the first brother be given Rs. P
=> Money with second brother = Rs. 1000 - P
Now, according to the question,
P [1 + (5 / 100)]
= (1000 - P) [1 + (5 / 100)]
=> P (1.05)
= (1000 - P) (1.05)
=> 0.9070 P = 1000 - P
=> 1.9070 P = 1000
=> P = 524.38
Therefore, share of first brother = Rs. 524.38
Share of second brother = Rs. 475.62
Question 4 : A sum of money amounts to Rs. 669 after 3 years and to Rs. 1003.50 after 6 years on compound interest. Find the sum.
Solution :
Let the sum of money be Rs. P
=> P [1 + (R/100)]
= 669 and P [1 + (R/100)]
= 1003.50
Dividing both equations, we get
[1 + (R/100)]
= 1003.50 / 669 = 1.50
Now, we put this value in the equation P [1 + (R/100)]
= 669
=> P x 1.50 = 669
=> P = 446
Thus, the required sum of money is Rs. 446
Question 5 : An investment doubles itself in 15 years if the interest is compounded annually. How many years will it take to become 8 times?
Solution :
It is given that the investment doubles itself in 15 years.
Let the initial investment be Rs. P
=> At the end of 15 years, A = 2 P
Now, this 2 P will be invested.
=> Amount after 15 more years = 2 x 2 P = 4 P
Now, this 4 P will be invested.
=> Amount after 15 more years = 2 x 4 P = 8 P
Thus, the investment (P) will become 8 times (8 P) in 15 + 15 + 15 = 45 years