Converse of the Pythagorean Theorem as name suggests, is converse statement of Pythagorean Theorem. Pythagorean Theorem itself states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. The converse of this theorem flips the logic. if a triangle has sides such that the square of the longest side is equal to the sum of the squares of the other two sides, then the triangle must be a right triangle.
In this article, we are going to discuss the converse of the Pythagorean theorem, its proof, and some solved examples based on them.
What is the Pythagorean Theorem?
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite to the right angle) is equal to the sum of the squares of the other two sides.
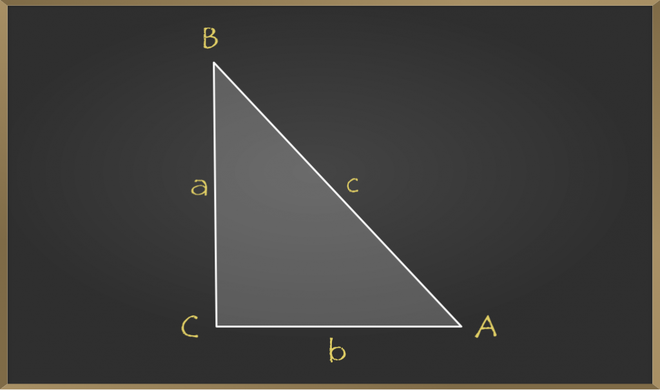
Mathematically, Pythagorean theorem can be stated as.
a2 + b2 = c2
Where.
a and b are other two sides of triangle and, c is hypotenuse of right triangle.
What is the Converse of the Pythagorean Theorem?
The converse of the Pythagorean theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle. It is simply the reverse of the original Pythagorean theorem. In simpler terms, if we are given a triangle and we know the length of all its three sides, we can check if it is a right-angled triangle or not by using the converse rule.
For Example. Let's suppose we are given an triangle with sides 5 cm, 12 cm, and 13 cm. We have to check if this is a right-angled triangle. We will use the converse of the Pythagorean Theorem to check.
First, we square the lengths of the sides.
- 52 = 25
- 122 = 144
- 132 = 169
Now we check if sum of square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides or not.
169 = 25 + 144
Since, the squares add up correctly, so given triangle is a right-angled triangle.
Proof of Converse of Pythagorean Theorem
We are going to see the proof of converse of Pythagorean theorem.
Statement. If in a triangle, the square of one side is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

Given Triangles in above Image.
Triangle ABC with ∠ACB = 90°
Triangle PQR with ∠PQR = 90°
Now, we identify the sides.
In triangle ABC. Hypotenuse is AB and the other two sides is AC and BC
In triangle PQR. Hypotenuse is PR and other two sides PQ and QR
Now, we know the Pythagorean theorem for each triangle.
For triangle ABC. AB2 =AC2 + BC2
For triangle PQR. PR2 = PQ2 + QR2
now, To prove the converse, let's assume that in triangle ABC.
AB2 = AC2 + BC2
And in triangle PQR.
PR2 = PQ2 + QR2
Since the square of the hypotenuse is equal to the sum of the squares of the other two sides in both triangles, the converse of the Pythagorean theorem states that these triangles must be right triangles.
Since triangles ABC and PQR satisfy the condition of the converse of the Pythagorean theorem, it is proven that they are right triangles with ∠ACB = 90° and ∠PQR = 90°, respectively.
Thus, the converse of the Pythagorean theorem is proven using the given triangles.
Solved Examples on Converse of the Pythagorean Theorem
Examples 1. Given a triangle ABC which has sides of lengths 7 cm, 24 cm, and 25 cm. Determine it if is a right-angled triangle or not.
Solution.
Given sides of length. 7 cm, 24 cm, and 25 cm
Square the sides.
72 = 49
242 = 576
252 = 625
Now, we check if the square of longest side is equal to sum of other two sides.
49 + 576 = 625
Since 625 = 625, triangle ABC is a right-angled triangle.
Examples 2. A triangle has sides 5 cm, 12 cm, and 14 cm. Use the converse of the Pythagorean Theorem to check if it’s right-angled or not.
Solution.
Given sides of length. 5 cm, 12 cm, and 14 cm
Square the sides.
52 = 25
122 = 144
142 = 196
Check.
25 + 144 = 169
169 ≠ 196
Since 169 ≠ 196, this triangle is not right-angled.
Examples 3. Given a triangle ABC which has sides of lengths 11 cm, 60 cm, and 61 cm. Determine if it is a right-angled triangle or not.
Solution.
Given sides of length. 11 cm, 60 cm, and 61 cm
Square the sides.
112 = 121
602 = 3600
612 = 3721
Now, we check if the square of the longest side is equal to the sum of the other two sides.
121 + 3600 = 3721
Since 3721 = 3721, triangle ABC is a right-angled triangle.
Examples 4. A triangle has sides 16 cm, 30 cm, and 34 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Solution.
Given sides of length. 16 cm, 30 cm, and 34 cm
Square the sides.
162 = 256
302 = 900
342 = 1156
Check.
256+900=1156
Since 1156=1156, this triangle is a right-angled triangle.
Practice Questions on Converse of Pythagorean Theorem
Q 1. A triangle has sides 9 cm, 12 cm, and 15 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Q 2. Given a triangle with sides of lengths 8 cm, 15 cm, and 17 cm. Determine if it is a right-angled triangle.
Q 3. A triangle has sides 10 cm, 24 cm, and 26 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Q 4. Given a triangle with sides of lengths 14 cm, 48 cm, and 50 cm. Determine if it is a right-angled triangle.
Q 5. A triangle has sides 12 cm, 16 cm, and 20 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Q 6. A triangle has sides 5 cm, 8 cm, and 10 cm. Determine if it is a right-angled triangle or not.
Q 7. Given a triangle with sides of lengths 21 cm, 28 cm, and 35 cm. Determine if it is a right-angled triangle.
Q 8. A triangle has sides 15 cm, 20 cm, and 25 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Q 9. Given a triangle with sides of lengths 18 cm, 24 cm, and 30 cm. Determine if it is a right-angled triangle.
Q 10. A triangle has sides 10 cm, 20 cm, and 22 cm. Use the Converse of the Pythagorean Theorem to check if it’s right-angled or not.
Answers.
1. Right-angled
2. Right-angled
3. Right-angled
4. Right-angled
5. Right-angled
6. Not right-angled
7. Right-angled
8. Right-angled
9. Right-angled
10. Not right-angled
Conclusion
The converse of the Pythagorean theorem is reverse theorem of Pythagorean theorem. It is an important concept of geometry mathematics. It is important to understand how we can apply this concept. We can use this concept to determine whether a triangle is right-angled if all its three sides are given. We should practice different questions based on this concept to understand this concept much better.
Read More,