C++ Program For Recursive Selection Sort For Singly Linked List - Swapping Node Links

Given a singly linked list containing n nodes. The problem is to sort the list using the recursive selection sort technique. The approach should be such that it involves swapping node links instead of swapping node data.

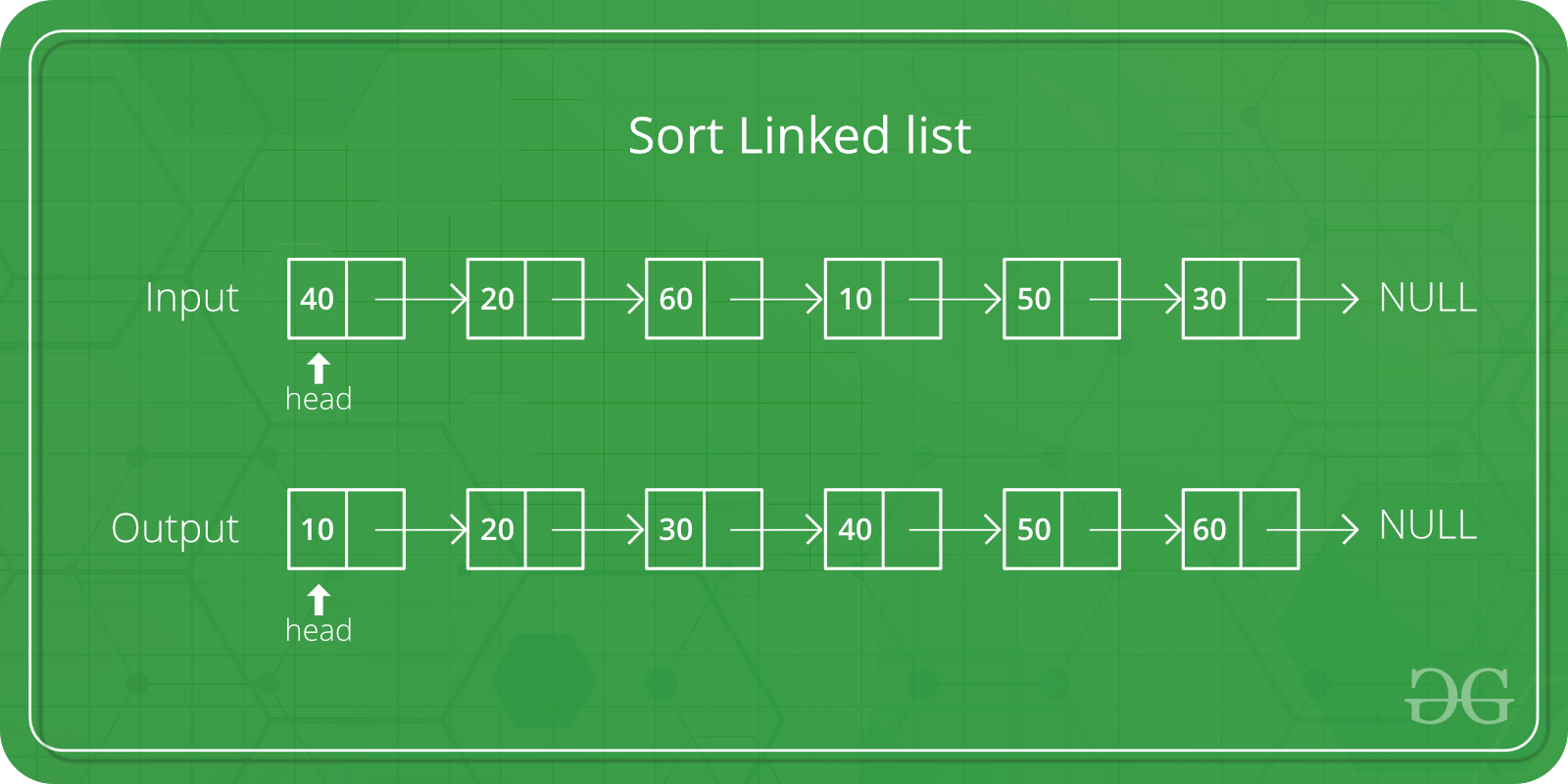
Examples:

Input: 10 -> 12 -> 8 -> 4 -> 6
Output: 4 -> 6 -> 8 -> 10 -> 12 

In Selection Sort, we first find the minimum element, swap it with the beginning node and recur for the remaining list. Below is the recursive implementation of these steps for the linked list. 

recurSelectionSort(head)
     if head->next == NULL
         return head
     Initialize min = head
     Initialize beforeMin = NULL
     Initialize ptr = head
    
     while ptr->next != NULL 
         if min->data > ptr->next->data
         min = ptr->next
         beforeMin = ptr
     ptr = ptr->next    
    
     if min != head
         swapNodes(&head, head, min, beforeMin)
    
     head->next = recurSelectionSort(head->next)
     return head

swapNodes(head_ref, currX, currY, prevY)
     head_ref = currY
     prevY->next = currX

     Initialize temp = currY->next
     currY->next = currX->next
     currX->next  = temp    

The swapNodes(head_ref, currX, currY, prevY) is based on the approach discussed here but it has been modified accordingly for the implementation of this post. 

C++

// C++ implementation of recursive 
// selection sort for singly linked 
// list | Swapping node links
#include <bits/stdc++.h>
using namespace std;

// A Linked list node
struct Node 
{
    int data;
    struct Node* next;
};

// Function to swap nodes 'currX' 
// and 'currY' in a linked list 
// without swapping data
void swapNodes(struct Node** head_ref, 
               struct Node* currX,
               struct Node* currY, 
               struct Node* prevY)
{
    // Make 'currY' as new head
    *head_ref = currY;

    // Adjust links
    prevY->next = currX;

    // Swap next pointers
    struct Node* temp = currY->next;
    currY->next = currX->next;
    currX->next = temp;
}

// Function to sort the linked list using
// recursive selection sort technique
struct Node* recurSelectionSort(struct Node* head)
{
    // If there is only a single node
    if (head->next == NULL)
        return head;

    // 'min' - pointer to store the node 
    // having minimum data value
    struct Node* min = head;

    // 'beforeMin' - pointer to store 
    // node previous to 'min' node
    struct Node* beforeMin = NULL;
    struct Node* ptr;

    // traverse the list till the last node
    for (ptr = head; ptr->next != NULL; 
         ptr = ptr->next) 
    {
        // if true, then update 'min' and 
        // 'beforeMin'
        if (ptr->next->data < min->data) 
        {
            min = ptr->next;
            beforeMin = ptr;
        }
    }

    // If 'min' and 'head' are not same,
    // swap the head node with the 'min' node
    if (min != head)
        swapNodes(&head, head, min, beforeMin);

    // Recursively sort the remaining list
    head->next = recurSelectionSort(head->next);

    return head;
}

// Function to sort the given linked list
void sort(struct Node** head_ref)
{
    // If list is empty
    if ((*head_ref) == NULL)
        return;

    // Sort the list using recursive 
    // selection sort technique
    *head_ref = recurSelectionSort(*head_ref);
}

// Function to insert a node at the
// beginning of the linked list
void push(struct Node** head_ref, 
          int new_data)
{
    // Allocate node
    struct Node* new_node = 
    (struct Node*)malloc(sizeof(struct Node));

    // Put in the data
    new_node->data = new_data;

    // Link the old list to the 
    // new node
    new_node->next = (*head_ref);

    // Move the head to point to 
    // the new node
    (*head_ref) = new_node;
}

// Function to print the linked list
void printList(struct Node* head)
{
    while (head != NULL) 
    {
        cout << head->data << " ";
        head = head->next;
    }
}

// Driver code
int main()
{
    struct Node* head = NULL;

    // Create linked list 
    // 10->12->8->4->6
    push(&head, 6);
    push(&head, 4);
    push(&head, 8);
    push(&head, 12);
    push(&head, 10);

    cout << 
    "Linked list before sorting:n";
    printList(head);

    // Sort the linked list
    sort(&head);

    cout << 
    "Linked list after sorting:n";
    printList(head);

    return 0;
}

Output:

Linked list before sorting:
10 12 8 4 6
Linked list after sorting:
4 6 8 10 12

Time Complexity: O(n²)

Auxiliary Space: O(n)

Please refer complete article on Recursive selection sort for singly linked list | Swapping node links for more details!

Create Quiz