Construct a tree from Inorder and Level order traversals | Set 2
Last Updated :
09 Oct, 2024
Given in-order and level-order traversals of a Binary Tree, the task is to construct the Binary Tree and return its root.
Example:
Input:
in[] = {4, 8, 10, 12, 14, 20, 22};
level[] = {20, 8, 22, 4, 12, 10, 14};
Output:
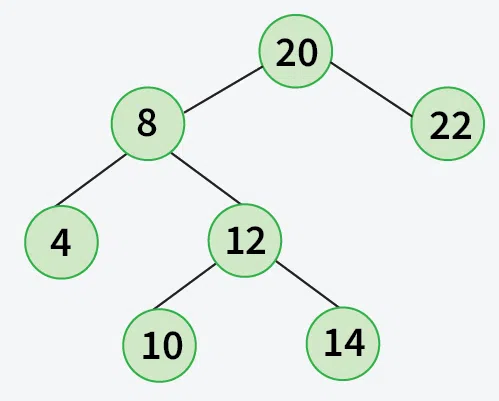
[Naive Approach] Using Recursion and hash map - O(n^2) Time and O(n) Space
The idea is to map the values of the in-order array to their respective indices in a hash map and construct the root node from the first element of the level order array. Find the index of this element in the in-order array using the hash map. Recursively create the left subtree from the elements present on the left side to the current element in the in-order array. Similarly, create the right subtree from the elements present on the right side to the current element in the in-order array.
Below is the implementation of the above approach:
C++
// c++ program to construct tree using
// inorder and levelorder traversals
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int key;
Node *left, *right;
Node(int x) {
key = x;
left = nullptr;
right = nullptr;
}
};
// Recursive function to build the binary tree.
Node* buildTreeRecur(unordered_map<int, int> map,
vector<int> &level, int s, int e) {
// For empty array, return null
if (s > e) {
return nullptr;
}
// create the root Node
Node* root = new Node(level[0]);
// find the index of the first element of level array
// in the in-order array.
int index = map[level[0]];
// find the number of elements which will be present in the
// left subtree and right subtree.
int lCnt = 0, rCnt = 0;
for (int i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) lCnt++;
else rCnt++;
}
// Level order vector for left and right subtree.
vector<int> lLevel(lCnt), rLevel(rCnt);
// add the left and right elements to lLevel and rLevel
int l = 0, r = 0;
for (int i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) {
lLevel[l++] = level[i];
}
else {
rLevel[r++] = level[i];
}
}
// Recursively create the left and right subtree.
root->left = buildTreeRecur(map, lLevel, s, index - 1);
root->right = buildTreeRecur(map, rLevel, index + 1, e);
return root;
}
// Main function
Node* buildTree(vector<int> &in, vector<int> &level, int n) {
// map the values of inorder
// vector to their indices.
unordered_map<int, int> inMap;
for (int i = 0; i < n; i++) {
inMap[in[i]] = i;
}
// Build the tree recursively.
Node* root = buildTreeRecur(inMap, level, 0, n - 1);
return root;
}
void printInorder(Node* head) {
Node* curr = head;
if (curr == nullptr)
return;
printInorder(curr->left);
cout << curr->key << " ";
printInorder(curr->right);
}
int main() {
vector<int> in = { 4, 8, 10, 12, 14, 20, 22 };
vector<int> level = { 20, 8, 22, 4, 12, 10, 14 };
int n = in.size();
Node* root = buildTree(in, level, n);
printInorder(root);
return 0;
}
// java program to construct tree using
// inorder and levelorder traversals
import java.util.*;
class Node {
int key;
Node left, right;
Node(int x) {
key = x;
left = right = null;
}
}
class GfG {
// Recursive function to build the binary tree.
static Node buildTreeRecur(HashMap<Integer, Integer> map,
ArrayList<Integer> level, int s, int e) {
// For empty array, return null
if (s > e) {
return null;
}
Node root = new Node(level.get(0));
// find the index of first element of
// level array in the in-order array.
int index = map.get(level.get(0));
// find the number of elements which
// will be present in the
// left subtree and right subtree.
int lCnt = 0, rCnt = 0;
for (int i = 1; i < e - s + 1; i++) {
if (map.get(level.get(i)) < index) lCnt++;
else rCnt++;
}
// Level order ArrayList for left and right subtree.
ArrayList<Integer> lLevel = new ArrayList<>(lCnt);
ArrayList<Integer> rLevel = new ArrayList<>(rCnt);
// add the left and right elements to lLevel and
// rLevel
int l = 0, r = 0;
for (int i = 1; i < e - s + 1; i++) {
if (map.get(level.get(i)) < index) {
lLevel.add(level.get(i));
} else {
rLevel.add(level.get(i));
}
}
// Recursively create the left and right subtree.
root.left =
buildTreeRecur(map, lLevel, s, index - 1);
root.right =
buildTreeRecur(map, rLevel, index + 1, e);
return root;
}
static Node buildTree(ArrayList<Integer> in,
ArrayList<Integer> level, int n) {
// map the values of inorder
// ArrayList to their indices.
HashMap<Integer, Integer> inMap = new HashMap<>();
for (int i = 0; i < n; i++) {
inMap.put(in.get(i), i);
}
// Build the tree recursively.
return buildTreeRecur(inMap, level, 0, n - 1);
}
static void printInorder(Node head) {
if (head == null) return;
printInorder(head.left);
System.out.print(head.key + " ");
printInorder(head.right);
}
public static void main(String[] args) {
ArrayList<Integer> in =
new ArrayList<>(Arrays.asList(4, 8, 10, 12, 14, 20, 22));
ArrayList<Integer> level =
new ArrayList<>(Arrays.asList(20, 8, 22, 4, 12, 10, 14));
int n = in.size();
Node root = buildTree(in, level, n);
printInorder(root);
}
}
# python program to construct tree using
# inorder and levelorder traversals
class Node:
def __init__(self, x):
self.key = x
self.left = None
self.right = None
# Recursive function to build the binary tree.
def buildTreeRecur(inMap, level, s, e):
# For empty array, return null
if s > e:
return None
root = Node(level[0])
# find the index of first element of level array
# in the in-order array.
index = inMap[level[0]]
# find the number of elements which will be present in the
# left subtree and right subtree.
lCnt = 0
rCnt = 0
for i in range(1, e - s + 1):
if inMap[level[i]] < index:
lCnt += 1
else:
rCnt += 1
# Level order array for left and right subtree.
lLevel = [0] * lCnt
rLevel = [0] * rCnt
# add the left and right elements to lLevel and
# rLevel
l = 0
r = 0
for i in range(1, e - s + 1):
if inMap[level[i]] < index:
lLevel[l] = level[i]
l += 1
else:
rLevel[r] = level[i]
r += 1
# Recursively create the left and
# right subtree.
root.left = buildTreeRecur(inMap, lLevel, s, index - 1)
root.right = buildTreeRecur(inMap, rLevel, index + 1, e)
return root
def buildTree(in_order, level_order, n):
# map the values of inorder
# array to their indices.
inMap = {in_order[i]: i for i in range(n)}
# Build the tree recursively.
return buildTreeRecur(inMap, level_order, 0, n - 1)
def printInorder(head):
if head is None:
return
printInorder(head.left)
print(head.key, end=" ")
printInorder(head.right)
if __name__ == "__main__":
in_order = [4, 8, 10, 12, 14, 20, 22]
level_order = [20, 8, 22, 4, 12, 10, 14]
n = len(in_order)
root = buildTree(in_order, level_order, n)
printInorder(root)
// C# Program to construct tree using
// inorder and levelorder traversals
using System;
using System.Collections.Generic;
class Node {
public int key;
public Node left, right;
public Node(int x) {
key = x;
left = null;
right = null;
}
}
class GfG {
// Recursive function to build the binary tree.
static Node BuildTreeRecur(Dictionary<int, int> map,
List<int> level, int s, int e) {
// For empty array, return null
if (s > e) {
return null;
}
Node root = new Node(level[0]);
// Find the index of first element of level list
// in the in-order list.
int index = map[level[0]];
// Find the number of elements which will
// be present in the left subtree and right subtree.
int lCnt = 0, rCnt = 0;
for (int i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) lCnt++;
else rCnt++;
}
// Level order lists for left and right subtree.
List<int> lLevel = new List<int>(lCnt);
List<int> rLevel = new List<int>(rCnt);
// Add the left and right elements to
// lLevel and rLevel
for (int i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) {
lLevel.Add(level[i]);
} else {
rLevel.Add(level[i]);
}
}
// Recursively create the left and right subtree
root.left = BuildTreeRecur(map, lLevel, s, index - 1);
root.right = BuildTreeRecur(map, rLevel, index + 1, e);
return root;
}
static Node BuildTree(List<int> inorder, List<int> level, int n) {
// Map the values of inorder list to their indices
Dictionary<int, int> inMap = new Dictionary<int, int>();
for (int i = 0; i < n; i++) {
inMap[inorder[i]] = i;
}
// Build the tree recursively
return BuildTreeRecur(inMap, level, 0, n - 1);
}
static void PrintInorder(Node node) {
if (node == null) return;
PrintInorder(node.left);
Console.Write(node.key + " ");
PrintInorder(node.right);
}
static void Main(string[] args) {
List<int> inorder = new List<int> { 4, 8, 10, 12, 14, 20, 22 };
List<int> level = new List<int> { 20, 8, 22, 4, 12, 10, 14 };
int n = inorder.Count;
Node root = BuildTree(inorder, level, n);
PrintInorder(root);
}
}
// JavaScript Program to construct tree using
// inorder and levelorder traversals
class Node {
constructor(x) {
this.key = x;
this.left = null;
this.right = null;
}
}
// Recursive function to build the binary tree
function buildTreeRecur(map, level, s, e) {
// For empty array, return null
if (s > e) {
return null;
}
let root = new Node(level[0]);
// Find the index of the first element of level array
// in the inorder array
let index = map[level[0]];
// Find the number of elements present in the
// left and right subtree
let lCnt = 0, rCnt = 0;
for (let i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) lCnt++;
else rCnt++;
}
// Level order array for left and right subtree
let lLevel = new Array(lCnt);
let rLevel = new Array(rCnt);
// Add the left and right elements to
// lLevel and rLevel
let l = 0, r = 0;
for (let i = 1; i < e - s + 1; i++) {
if (map[level[i]] < index) {
lLevel[l++] = level[i];
} else {
rLevel[r++] = level[i];
}
}
// Recursively create the left and
// right subtree
root.left = buildTreeRecur(map, lLevel, s, index - 1);
root.right = buildTreeRecur(map, rLevel, index + 1, e);
return root;
}
// Main function to build the tree
function buildTree(inorder, level, n) {
// Map the values of inorder array to
// their indices
let inMap = {};
for (let i = 0; i < n; i++) {
inMap[inorder[i]] = i;
}
// Build the tree recursively
return buildTreeRecur(inMap, level, 0, n - 1);
}
function printInorder(node) {
if (node === null) return;
printInorder(node.left);
console.log(node.key);
printInorder(node.right);
}
let inorder = [4, 8, 10, 12, 14, 20, 22];
let level = [20, 8, 22, 4, 12, 10, 14];
let n = inorder.length;
let root = buildTree(inorder, level, n);
printInorder(root);
[Alternate Approach] Using Recursion and Hast Set - O(n^2) Time and O(n) Space
The idea is to construct the root node from the first element of the level order array. Find the index of this element in the in-order array. Then, find the elements in level order array which will be present in left subtree and right subtree using a hashset (Insert the left subtree elements from in-order array in set, then traverse the level-order array and check if the element will be present in left subtree or right subtree). Recursively create the left subtree and right subtree from the elements present on the left and right side to the current element in the in-order array.
Below is the implementation of the above approach:
C++
// c++ program to construct tree using
// inorder and levelorder traversals
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int key;
Node *left, *right;
Node(int x) {
key = x;
left = nullptr;
right = nullptr;
}
};
// Function to find the index of an element.
int searchValue(vector<int> in, int value, int s, int e) {
for (int i=s; i<=e; i++) {
if (in[i] == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
Node* buildTreeRecur(vector<int> in, vector<int> level, int s, int e) {
// For empty array, return null
if (s>e) {
return nullptr;
}
Node* root = new Node(level[0]);
// find the index of first element of level array
// in the in-order array.
int index = searchValue(in, level[0], s, e);
int lCnt = index-s, rCnt = e - index;
// Level order array for left and right subtree.
vector<int> lLevel(lCnt);
vector<int> rLevel(rCnt);
// insert the left subtree elements
// into the set.
unordered_set<int> set;
for (int i=s; i<index; i++) {
set.insert(in[i]);
}
// add the left and right elements to lLevel and
// rLevel
int l = 0, r = 0;
for (int i=1; i< e-s+1; i++) {
// If the value is present in
// left subtree.
if (set.find(level[i]) != set.end())
lLevel[l++] = level[i];
// else it will be present in
// right subtree.
else
rLevel[r++] = level[i];
}
// Recursively create the left and right subtree.
root->left = buildTreeRecur(in, lLevel, s, index-1);
root->right = buildTreeRecur(in, rLevel, index+1, e);
return root;
}
// Main function
Node* buildTree(vector<int> inorder, vector<int> level, int n) {
// Build the tree recursively.
Node* root = buildTreeRecur(inorder, level, 0, n-1);
return root;
}
void printInorder(Node* head) {
Node* curr = head;
if (curr == nullptr)
return;
printInorder(curr->left);
cout << curr->key << " ";
printInorder(curr->right);
}
int main() {
vector<int> in = { 4, 8, 10, 12, 14, 20, 22 };
vector<int> level = { 20, 8, 22, 4, 12, 10, 14 };
int n = level.size();
Node* root = buildTree(in, level, n);
printInorder(root);
return 0;
}
// Java program to construct tree using
// inorder and levelorder traversals
import java.util.ArrayList;
import java.util.HashSet;
import java.util.Set;
class Node {
public int key;
public Node left, right;
public Node(int x) {
key = x;
left = null;
right = null;
}
}
class GfG {
// Function to find the index of an element.
static int searchValue(ArrayList<Integer> in,
int value, int s, int e) {
for (int i = s; i <= e; i++) {
if (in.get(i) == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
static Node buildTreeRecur(ArrayList<Integer> in,
ArrayList<Integer> level, int s, int e) {
// For empty array, return null
if (s > e) {
return null;
}
// create the root Node
Node root = new Node(level.get(0));
// find the index of first element of level array
// in the in-order array.
int index = searchValue(in, level.get(0), s, e);
int lCnt = index - s, rCnt = e - index;
// Level order array for left and right subtree.
ArrayList<Integer> lLevel = new ArrayList<>(lCnt);
ArrayList<Integer> rLevel = new ArrayList<>(rCnt);
// insert the left subtree elements
// into the set.
Set<Integer> set = new HashSet<>();
for (int i = s; i < index; i++) {
set.add(in.get(i));
}
// add the left and right elements to lLevel and
// rLevel
int l = 0, r = 0;
for (int i = 1; i < e - s + 1; i++) {
// If the value is present in
// left subtree.
if (set.contains(level.get(i)))
lLevel.add(level.get(i));
// else it will be present in
// right subtree.
else
rLevel.add(level.get(i));
}
// Recursively create the left and
// right subtree.
root.left = buildTreeRecur(in, lLevel, s, index - 1);
root.right = buildTreeRecur(in, rLevel, index + 1, e);
return root;
}
// Main function
static Node buildTree(ArrayList<Integer> inorder,
ArrayList<Integer> level, int n) {
// Build the tree recursively.
return buildTreeRecur(inorder, level, 0, n - 1);
}
static void printInorder(Node head) {
Node curr = head;
if (curr == null)
return;
printInorder(curr.left);
System.out.print(curr.key + " ");
printInorder(curr.right);
}
public static void main(String[] args) {
ArrayList<Integer> in =
new ArrayList<>(java.util.Arrays.asList(4, 8, 10, 12, 14, 20, 22));
ArrayList<Integer> level =
new ArrayList<>(java.util.Arrays.asList(20, 8, 22, 4, 12, 10, 14));
int n = level.size();
Node root = buildTree(in, level, n);
printInorder(root);
}
}
# Python program to construct tree using
# inorder and levelorder traversals
class Node:
def __init__(self, x):
self.key = x
self.left = None
self.right = None
# Function to find the index of an element.
def searchValue(inorder, value, s, e):
for i in range(s, e + 1):
if inorder[i] == value:
return i
return -1
# Recursive function to build the binary tree.
def buildTreeRecur(inorder, level, s, e):
# For empty array, return null
if s > e:
return None
# create the root Node
root = Node(level[0])
# find the index of first element of level array
# in the in-order array.
index = searchValue(inorder, level[0], s, e)
l_cnt = index - s
r_cnt = e - index
# Level order array for left and right subtree.
l_level = []
r_level = []
# insert the left subtree elements
# into the set.
s_set = set(inorder[s:index])
# add the left and right elements to l_level and
# r_level
for i in range(1, e - s + 1):
# If the value is present in
# left subtree.
if level[i] in s_set:
l_level.append(level[i])
# else it will be present in
# right subtree.
else:
r_level.append(level[i])
# Recursively create the left and
# right subtree.
root.left = buildTreeRecur(inorder, l_level, s, index - 1)
root.right = buildTreeRecur(inorder, r_level, index + 1, e)
return root
# Main function
def buildTree(inorder, level, n):
# Build the tree recursively.
return buildTreeRecur(inorder, level, 0, n - 1)
def printInorder(root):
if root is None:
return
printInorder(root.left)
print(root.key, end=" ")
printInorder(root.right)
if __name__ == "__main__":
inorder = [4, 8, 10, 12, 14, 20, 22]
level = [20, 8, 22, 4, 12, 10, 14]
n = len(level)
root = buildTree(inorder, level, n)
printInorder(root)
// C# program to construct tree using
// inorder and levelorder traversals
using System;
using System.Collections.Generic;
class Node {
public int key;
public Node left, right;
public Node(int x) {
key = x;
left = null;
right = null;
}
}
// Function to find the index of an element.
class GfG {
static int SearchValue(List<int> inorder,
int value, int s, int e) {
for (int i = s; i <= e; i++) {
if (inorder[i] == value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
static Node BuildTreeRecur(List<int> inorder,
List<int> level, int s, int e) {
// For empty array, return null
if (s > e) {
return null;
}
Node root = new Node(level[0]);
// find the index of first element of level array
// in the in-order array.
int index = SearchValue(inorder, level[0], s, e);
int lCnt = index - s, rCnt = e - index;
// Level order array for left and right subtree.
List<int> lLevel = new List<int>(lCnt);
List<int> rLevel = new List<int>(rCnt);
// insert the left subtree elements
// into the set.
HashSet<int> set = new HashSet<int>();
for (int i = s; i < index; i++) {
set.Add(inorder[i]);
}
// add the left and right elements to lLevel and
// rLevel
for (int i = 1; i < e - s + 1; i++) {
// If the value is present in
// left subtree.
if (set.Contains(level[i]))
lLevel.Add(level[i]);
// else it will be present in
// right subtree.
else
rLevel.Add(level[i]);
}
// Recursively create the left and right subtree.
root.left = BuildTreeRecur(inorder, lLevel, s, index - 1);
root.right = BuildTreeRecur(inorder, rLevel, index + 1, e);
return root;
}
// Main function
static Node BuildTree(List<int> inorder, List<int> level, int n) {
// Build the tree recursively.
return BuildTreeRecur(inorder, level, 0, n - 1);
}
static void PrintInorder(Node head) {
if (head == null)
return;
PrintInorder(head.left);
Console.Write(head.key + " ");
PrintInorder(head.right);
}
static void Main(string[] args) {
List<int> inorder = new List<int> { 4, 8, 10, 12, 14, 20, 22 };
List<int> level = new List<int> { 20, 8, 22, 4, 12, 10, 14 };
int n = level.Count;
Node root = BuildTree(inorder, level, n);
PrintInorder(root);
}
}
// JavaScript program to construct tree using
// inorder and levelorder traversals
class Node {
constructor(x) {
this.key = x;
this.left = null;
this.right = null;
}
}
// Function to find the index of an element.
function searchValue(inorder, value, s, e) {
for (let i = s; i <= e; i++) {
if (inorder[i] === value)
return i;
}
return -1;
}
// Recursive function to build the binary tree.
function buildTreeRecur(inorder, level, s, e) {
// For empty array, return null
if (s > e) {
return null;
}
let root = new Node(level[0]);
// find the index of first element of level array
// in the in-order array.
let index = searchValue(inorder, level[0], s, e);
let lCnt = index - s, rCnt = e - index;
// Level order array for left and
// right subtree.
let lLevel = [];
let rLevel = [];
// insert the left subtree elements
// into the set.
let set = new Set();
for (let i = s; i < index; i++) {
set.add(inorder[i]);
}
// add the left and right elements to lLevel and
// rLevel
for (let i = 1; i < e - s + 1; i++) {
// If the value is present in
// left subtree.
if (set.has(level[i]))
lLevel.push(level[i]);
// else it will be present in
// right subtree.
else
rLevel.push(level[i]);
}
// Recursively create the left and right subtree.
root.left = buildTreeRecur(inorder, lLevel, s, index - 1);
root.right = buildTreeRecur(inorder, rLevel, index + 1, e);
return root;
}
// Main function
function buildTree(inorder, level, n) {
// Build the tree recursively.
return buildTreeRecur(inorder, level, 0, n - 1);
}
function printInorder(root) {
if (root === null)
return;
printInorder(root.left);
console.log(root.key + " ");
printInorder(root.right);
}
const inorder = [4, 8, 10, 12, 14, 20, 22];
const level = [20, 8, 22, 4, 12, 10, 14];
const n = level.length;
const root = buildTree(inorder, level, n);
printInorder(root);
[Expected Approach] Using Queue and Hash map- O(n) Time and O(n) Space
The idea is to use the first element in level order array to create the root node. Find the index of the same element in the in-order array. If elements are present on the left side, then create root->left node. Similarly, if elements are present on the right side, then create root->right node.
Step by step implementation:
- As the first level of tree only consists of root node, so use the first element in the level array to create the root node.
- Push this root node into a queue with some other information, s: It denotes the start index of the current segment in in-order traversal while e denotes the last index of the current segment in in-order traversal.
- While q is not empty , follow below
- Pop the the front node of the queue. Find the index of this node (currIndex) in the in-order traversal.
- If s < currIndex, it means there is at least one element in left subtree of this node. So create node->left = level[index] and increment index. Also push {node->left, s, currIndex-1} into the queue.
- if currIndex < e, then it means that there is at least one element in right subtree of this node. So create node->right= level[index] and increment index. Also push {node->right, currIndex+1, e} into the queue.
Below is the implementation of the above approach:
C++
// c++ program to construct tree using
// inorder and levelorder traversals
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int key;
Node *left, *right;
Node(int x) {
key = x;
left = right = nullptr;
}
};
class Data {
public:
Node* node;
int s, e;
Data(Node* n, int s, int e) {
this->node = n;
this->s = s;
this->e = e;
}
};
// Function which builds the tree
Node* buildTree(vector<int>& in,
vector<int>& level, int n) {
// return null if tree is empty
if (n == 0) return nullptr;
// Hashmap which will map the values
// to its respective index.
unordered_map<int, int> map;
for (int i = 0; i < n; i++) {
map[in[i]] = i;
}
// Create the root node.
Node* root = new Node(level[0]);
int index = 1;
// Push the root node into the queue.
queue<Data*> q;
q.push(new Data(root, 0, n - 1));
// This queue will traverse the nodes
// in level order manner
while (!q.empty()) {
Data* curr = q.front();
q.pop();
int s = curr->s, e = curr->e;
Node* node = curr->node;
int currIndex = map[node->key];
// If elements exist to the left of current
// node in inorder array, then left node will
// exist.
if (s < currIndex) {
Node* tmp = new Node(level[index++]);
node->left = tmp;
q.push(new Data(tmp, s, currIndex - 1));
}
// If elements exist to the right of current
// node in inorder array, then right node will
// exist.
if (currIndex < e) {
Node* tmp = new Node(level[index++]);
node->right = tmp;
q.push(new Data(tmp, currIndex + 1, e));
}
}
// return the root node.
return root;
}
void printInorder(Node* node) {
if (node == nullptr)
return;
printInorder(node->left);
cout << node->key << " ";
printInorder(node->right);
}
int main() {
vector<int> in = { 4, 8, 10, 12, 14, 20, 22 };
vector<int> level = { 20, 8, 22, 4, 12, 10, 14 };
int n = in.size();
Node* root = buildTree(in, level, n);
printInorder(root);
return 0;
}
// java program to construct tree using
// inorder and levelorder traversals
import java.util.*;
class Node {
int key;
Node left, right;
Node(int x) {
key = x;
left = right = null;
}
}
class Data {
Node node;
int s, e;
Data(Node n, int s, int e) {
this.node = n;
this.s = s;
this.e = e;
}
}
class GfG {
// Function which builds the tree
static Node buildTree(ArrayList<Integer> in,
ArrayList<Integer> level, int n) {
// return null if tree is empty
if (n == 0) return null;
// Hashmap which will map the values to its
// respective index
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
map.put(in.get(i), i);
}
// Create the root node
Node root = new Node(level.get(0));
int index = 1;
Queue<Data> q = new LinkedList<>();
// Push the root node into the queue
q.add(new Data(root, 0, n - 1));
// This queue will traverse the nodes in
// level order manner
while (!q.isEmpty()) {
Data curr = q.poll();
int s = curr.s, e = curr.e;
Node node = curr.node;
int currIndex = map.get(node.key);
// If elements exist to the left of current
// node in inorder array, then left node will
// exist.
if (s < currIndex) {
Node tmp = new Node(level.get(index++));
node.left = tmp;
q.add(new Data(tmp, s, currIndex - 1));
}
// If elements exist to the right of current
// node in inorder array, then right node will
// exist.
if (currIndex < e) {
Node tmp = new Node(level.get(index++));
node.right = tmp;
q.add(new Data(tmp, currIndex + 1, e));
}
}
// return the root node
return root;
}
static void printInorder(Node node) {
if (node == null) return;
printInorder(node.left);
System.out.print(node.key + " ");
printInorder(node.right);
}
public static void main(String[] args) {
ArrayList<Integer> in =
new ArrayList<>(Arrays.asList(4, 8, 10, 12, 14, 20, 22));
ArrayList<Integer> level =
new ArrayList<>(Arrays.asList(20, 8, 22, 4, 12, 10, 14));
int n = in.size();
Node root = buildTree(in, level, n);
printInorder(root);
}
}
# python program to construct tree using
# inorder and levelorder traversals
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
class Data:
def __init__(self, node, s, e):
self.node = node
self.s = s
self.e = e
# Function which builds the tree
def buildTree(inorder, level, n):
# return None if tree is empty
if n == 0:
return None
# Hashmap which will map the values to its
# respective index
index_map = {inorder[i]: i for i in range(n)}
# Create the root node
root = Node(level[0])
index = 1
# Queue to hold Data
queue = [Data(root, 0, n - 1)]
# This queue will traverse the nodes in level
# order manner
while queue:
curr = queue.pop(0)
s, e = curr.s, curr.e
node = curr.node
currIndex = index_map[node.key]
# If elements exist to the left of current node
# in inorder array, then left node will
# exist.
if s < currIndex:
tmp = Node(level[index])
index += 1
node.left = tmp
queue.append(Data(tmp, s, currIndex - 1))
# If elements exist to the right of current
# node in inorder array, then right node will
# exist.
if currIndex < e:
tmp = Node(level[index])
index += 1
node.right = tmp
queue.append(Data(tmp, currIndex + 1, e))
# return the root node
return root
def printInorder(node):
if node is None:
return
printInorder(node.left)
print(node.key, end=" ")
printInorder(node.right)
if __name__ == '__main__':
inorder = [4, 8, 10, 12, 14, 20, 22]
level = [20, 8, 22, 4, 12, 10, 14]
n = len(inorder)
root = buildTree(inorder, level, n)
printInorder(root)
// c# program to construct tree using
// inorder and levelorder traversals
using System;
using System.Collections.Generic;
class Node {
public int key;
public Node left, right;
public Node(int x) {
key = x;
left = right = null;
}
}
class Data {
public Node node;
public int s, e;
public Data(Node n, int s, int e) {
node = n;
this.s = s;
this.e = e;
}
}
class GfG {
// Function which builds the tree
static Node buildTree(List<int> inorder, List<int> level, int n) {
// return null if tree is empty
if (n == 0) return null;
// Dictionary to map the values to its
// respective index
Dictionary<int, int> map = new Dictionary<int, int>();
for (int i = 0; i < n; i++) {
map[inorder[i]] = i;
}
// Create the root node
Node root = new Node(level[0]);
int index = 1;
// Queue to hold Data
Queue<Data> q = new Queue<Data>();
// Push the root node into the queue
q.Enqueue(new Data(root, 0, n - 1));
// This queue will traverse the nodes
// in level order manner
while (q.Count > 0) {
Data curr = q.Dequeue();
int s = curr.s, e = curr.e;
Node node = curr.node;
int currIndex = map[node.key];
// If elements exist to the left of current
// node in inorder list, then left node will
// exist.
if (s < currIndex) {
Node tmp = new Node(level[index++]);
node.left = tmp;
q.Enqueue(new Data(tmp, s, currIndex - 1));
}
// If elements exist to the right of current
// node in inorder list, then right node will
// exist.
if (currIndex < e) {
Node tmp = new Node(level[index++]);
node.right = tmp;
q.Enqueue(new Data(tmp, currIndex + 1, e));
}
}
// return the root node
return root;
}
static void printInorder(Node node) {
if (node == null) return;
printInorder(node.left);
Console.Write(node.key + " ");
printInorder(node.right);
}
static void Main(string[] args) {
List<int> inorder = new List<int> { 4, 8, 10, 12, 14, 20, 22 };
List<int> level = new List<int> { 20, 8, 22, 4, 12, 10, 14 };
int n = inorder.Count;
Node root = buildTree(inorder, level, n);
printInorder(root);
}
}
// javascript program to construct tree using
// inorder and levelorder traversals
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
}
class Data {
constructor(node, s, e) {
this.node = node;
this.s = s;
this.e = e;
}
}
// Function which builds the tree
function buildTree(inorder, level, n) {
// return null if tree is empty
if (n === 0) return null;
// Map which will map the values to
// its respective index
let map = new Map();
for (let i = 0; i < n; i++) {
map.set(inorder[i], i);
}
// Create the root node
let root = new Node(level[0]);
let index = 1;
// Queue to hold Data
let queue = [];
// Push the root node into the queue
queue.push(new Data(root, 0, n - 1));
// This queue will traverse the nodes
// in level order manner
while (queue.length > 0) {
let curr = queue.shift();
let s = curr.s, e = curr.e;
let node = curr.node;
let currIndex = map.get(node.key);
// If elements exist to the left of current
// node in inorder array, then left node will
// exist.
if (s < currIndex) {
let tmp = new Node(level[index++]);
node.left = tmp;
queue.push(new Data(tmp, s, currIndex - 1));
}
// If elements exist to the right of current
// node in inorder array, then right node will
// exist.
if (currIndex < e) {
let tmp = new Node(level[index++]);
node.right = tmp;
queue.push(new Data(tmp, currIndex + 1, e));
}
}
// return the root node
return root;
}
function printInorder(node) {
if (node === null) return;
printInorder(node.left);
console.log(node.key);
printInorder(node.right);
}
const inorder = [4, 8, 10, 12, 14, 20, 22];
const level = [20, 8, 22, 4, 12, 10, 14];
const n = inorder.length;
const root = buildTree(inorder, level, n);
printInorder(root);
Related articles:
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem